
uitgewerkt
$ \left\{ \begin{gathered} x_1 + 3x_2 + 4x_3 = 8 \\ x_1 + 2x_2 + 5x_3 = 13 \\ 3x_1 + x_2 - x_3 = 1 \\ \end{gathered} \right. $
$ \left( {\left. {\begin{array}{*{20}c} 1 & 3 & 4 \\ 1 & 2 & 5 \\ 3 & 1 & { - 1} \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 8 \\ {13} \\ 1 \\ \end{array} } \right) \to \left( {\left. {\begin{array}{*{20}c} 1 & 3 & 4 \\ 0 & { - 1} & 1 \\ 0 & { - 8} & { - 13} \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 8 \\ 5 \\ { - 23} \\ \end{array} } \right) $
$ \left( {\left. {\begin{array}{*{20}c} 1 & 3 & 4 \\ 0 & { - 1} & 1 \\ 0 & { - 8} & { - 13} \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 8 \\ 5 \\ { - 23} \\ \end{array} } \right) \to \left( {\left. {\begin{array}{*{20}c} 1 & 3 & 4 \\ 0 & { - 1} & 1 \\ 0 & 0 & { - 21} \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 8 \\ 5 \\ { - 63} \\ \end{array} } \right) $
$ \left( {\left. {\begin{array}{*{20}c} 1 & 3 & 4 \\ 0 & 1 & { - 1} \\ 0 & 0 & 1 \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 8 \\ { - 5} \\ 3 \\ \end{array} } \right) \to \left( {\left. {\begin{array}{*{20}c} 1 & 0 & 7 \\ 0 & 1 & { - 1} \\ 0 & 0 & 1 \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} {23} \\ { - 5} \\ 3 \\ \end{array} } \right) $
$ \left( {\left. {\begin{array}{*{20}c} 1 & 0 & 7 \\ 0 & 1 & { - 1} \\ 0 & 0 & 1 \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} {23} \\ { - 5} \\ 3 \\ \end{array} } \right) \to \left( {\left. {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right|} \right.\left. {\begin{array}{*{20}c} 2 \\ { - 2} \\ 3 \\ \end{array} } \right) $
$ \left\{ \begin{gathered} x = 2 \\ y = - 2 \\ z = 3 \\ \end{gathered} \right. $
Met de GR
Zet de aangevulde matrix in A
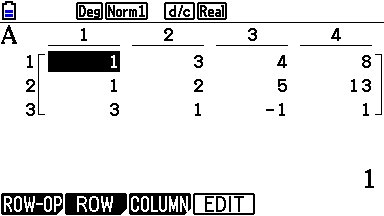
Met Rref Mat A krijg je dit:
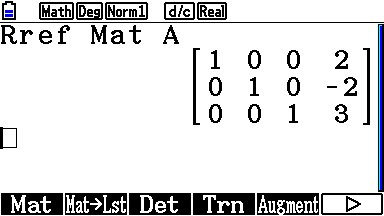



©2004-2026 Wiskundeleraar - login
|