Lineaire vergelijkingen met twee variabelen

De algemene vorm van een lineaire vergelijking met de variabelen $x$ en $y$:

$ax+by=c$

De grafiek van $ax+by=c$ is een rechte lijn. Om de lijn $k:3x-4y=12$ te tekenen kan je een tabel maken:

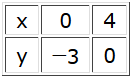
De lijn gaat door de punten $(0,-3)$ en $(4,0)$.

Oplossingen van ax+by=c

Het getallenpaar $(x,y)=(12,6)$ is een oplossing van $3x-4y=12$, want invullen geeft:

$3\cdot12-4\cdot6=12$

...en dat klopt...

Dus $(x,y)=(12,6)$ voldoet aan $3x-4y=12$ en het punt $(12,6)$ ligt op de lijn $3x-4y=12$.

Het opstellen van een lineaire vergelijking

Bij een pretpark is de toegangsprijs voor een volwassene €17 en voor een kind €12. Op een dag is er €19.200 aan entreegeld binnengekomen. Met x:aantal volwassenen en y:aantal kinderen geeft dat:

• $17x+12y=19.200$

Stelsels oplossen

• Elimineren door optellen en aftrekken

Voorbeeld 1

$
\eqalign{
  & \left\{ \matrix{
  3x - 5y = 18 \cr
  x - 3y = 14 \cr}  \right.  \cr
  & \left\{ \matrix{
  3x - 5y = 18\,\,\,(1) \cr
  3x - 9y = 42\,\,\,(2) \cr}  \right.  \cr
  & (1) - (2)\,\,geeft:  \cr
  & 4y =  - 24  \cr
  & y =  - 6  \cr
  & Invullen\,\,geeft:  \cr
  & x =  - 4 \cr}
$

De oplossing is $(x,y)=(-4,-6)$

Stelsels oplossen

• Elimineren door substitutie

Voorbeeld 2

$
\eqalign{
  & \left\{ \matrix{
  x =  - 3y + 2 \cr
  2x - y = 11 \cr}  \right.  \cr
  & 2\left( { - 3y + 2} \right) - y = 11  \cr
  &  - 6y + 4 - y = 11  \cr
  &  - 7y = 7  \cr
  & y =  - 1  \cr
  & x =  - 3 \cdot  - 1 + 2 = 5  \cr
  & \left\{ \matrix{
  x = 5 \cr
  y =  - 1 \cr}  \right. \cr}
$

De oplossing is $(x,y)=(5,-1)$