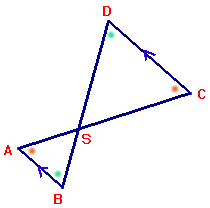
Snavelfiguren en zandloperfiguren
|
$ |
$ |
Je moet altijd toelichten waarom driehoeken gelijkvormig zijn. Je noteert daartoe de paren gelijke hoeken.
Zorg dat je bij de notatie van gelijkvormigheid de letters van de hoekpunten corresponderen met de overeenkomstige hoeken. Dat maakt het opstellen van de verhoudigstabel een stuk gemakkelijker.
Opgave 1
Gegeven: twee gelijkvormige rechthoeken. De eerste rechthoek is 2 bij 5 en de andere rechthoek is 10 bij p.
- Gevraagd: wat is p?
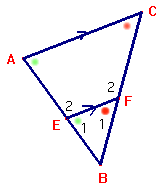
Opgave 2
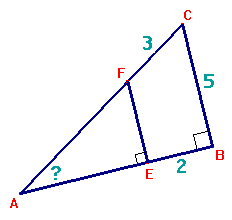
Gegeven: FC=3, EB=2 en BC=5
Gevraagd: bereken $\angle A$
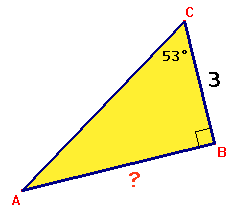
Goniometrische berekeningen
Het rekenen met goniometrische verhoudingen met een verhoudingstabel is niet zo handig. Dat kan gemakkelijker. Hieronder kan je daar 3 voorbeelden van vinden.
|
|
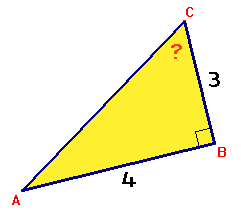
$ \eqalign{ & \tan \angle C = \frac{{AB}} {{BC}} \cr & \tan \angle C = \frac{4} {3} \cr & \angle C \approx 53^\circ \cr} $ |
|
|
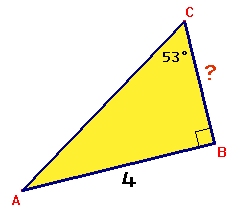
$ \eqalign{ & \tan \angle C = \frac{{AB}} {{BC}} \cr & \tan 53^\circ = \frac{4} {x} \cr & x = \frac{4} {{\tan 53^\circ }} \approx 3 \cr} $ |
|
|
$ \eqalign{ & \tan \angle C = \frac{{AB}} {{BC}} \cr & \tan 53^\circ = \frac{x} {3} \cr & x = 3 \cdot \tan 53^\circ \approx 4 \cr} $ |
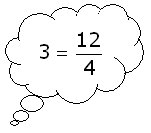 Als je dat lastig vindt dan kun je denken aan:
Als je dat lastig vindt dan kun je denken aan:
$\eqalign{3=\frac{12}{4}}$
Wat moet je met $12$ en $3$ doen als je de $4$ niet weet? Enz....