|
Gemiddelde en standaardafwijking van een proportie
Bij een steekproevenverdeling is de steekproefproportie $\widehat p$ bij een voldoende grote steekproef $n$ bij benadering normaal verdeeld.
Hierbij is het gemiddelde $\mu$ gelijk aan de populatieproportie.
Voor de standaardafwijking $\sigma$ geldt:
$\eqalign{\sigma=\sqrt{\frac{\widehat p(1-\widehat p)}{n}}}$
Voorbeeld 1
Men neemt 800 steekproeven van lengte 250 bij een populatieproportie van 0,350. Hieruit volgt dat de bijbehorende standaardafwijking gelijk is aan 0,030.
$n=250$ en $\widehat p=p=0,350$ geeft:
$\eqalign{\sigma=\sqrt{\frac{0,350\cdot0,650}{250}}}=0,0301...\approx0,030$
Berekening van de steekproefomvang
Je kunt bij een gegeven betrouwbaarheidsinterval de steekproefomvang berekenen.
Aanpak
-
Bepaal $\widehat p$ en $\sigma$
-
Stel met de formule een vergelijking op
-
Los de vergelijking op met je GR.
|
Steekproef en betrouwbaarheidsinterval
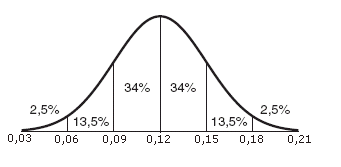
Het 95%-betrouwbaarheidsinterval geeft aan dat bij het steeds nemen van een nieuwe aselecte steekproef uit dezelfde populatie 95% van de daarbij opgestelde intervallen de populatieproportie bevat.
Het 95%-betrouwbaarheidsinterval is:
-
$[\widehat p-2\sigma,\widehat p+2\sigma]$
Hierin is $\widehat p$ de steekproefproportie en $\sigma$ de standaardafwijking.
Het 68%-betrouwbaarheidsinterval is:
-
$[\widehat p-\sigma,\widehat p+\sigma]$
Voorbeeld 2
Twee dagen voor de verkiezingen voor de Tweede Kamer wordt aan 1200 stemgerechtigde Nederlanders gevraagd of ze van plan zijn te gaan stemmen. Van deze 1200 zeggen 756 inderdaad te gaan stemmen
-
Bereken het 95%-betrouwbaarheidsinterval van de stemgerechtigde Nederlanders die van plan zijn te gaan stemmen.
Uitgewerkt
$\eqalign{\widehat p=\frac{756}{1200}\approx0,63}$ en $\eqalign{\sigma=\sqrt{\frac{0,63\cdot0,37}{1200}}\approx0,013937...}$
Het 95%-betrouwbaarheidsinterval is $[0,602;0,658]$
|