De grafiek van f heeft de lijn x=a als symmetrie-as als voor elke waarde van p geldt: |
|
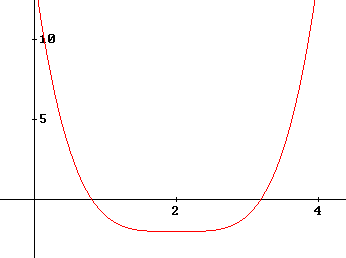
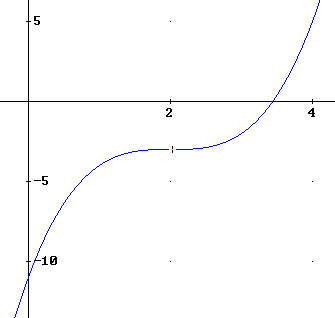
$ \eqalign{ & f(x) = (x - 2)^4 - 2 \cr & Heeft\,\,als\,\,symmetrie - as:x = 2 \cr & Er\,\,geldt:f(2 + p) = f(2 - p)\,\,voor\,\,p \in R \cr & f(2 + p) = f(2 - p) \cr & (2 + p - 2)^4 - 2 = (2 - p - 2)^4 - 2 \cr & p^4 - 2 = \left( { - p} \right)^4 - 2 \cr & Klopt! \cr} $ |
 |
De grafiek van f is puntsymmetrisch in het punt (a,b) als het gemiddelde van f(a+p) en f(a-p) gelijk is aan b voor elke waarde van p. |
|
$ \eqalign{ & f(x) = \left( {x - 2} \right)^3 - 3 \cr & Is\,\,puntsymmetrisch\,\,in\,\,(2, - 3): \cr & Er\,\,geldt:\frac{{f(2 + p) + f(2 - p)}} {2} = - 3 \cr & \frac{{\left( {2 + p - 2} \right)^3 - 3 + \left( {2 - p - 2} \right)^3 - 3}} {2} = \cr & \frac{{\left( p \right)^3 - 3 + \left( { - p} \right)^3 - 3}} {2} = \cr & \frac{{p^3 - 3 - p^3 - 3}} {2} = \cr & \frac{{ - 6}} {2} = - 3 \cr & Klopt! \cr} $ |
 |