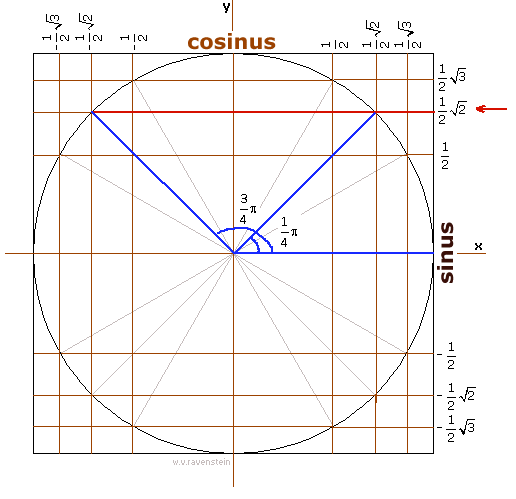
Voor welke $\alpha$ geldt: $\sin\alpha=\frac{1}{2}\sqrt{2}$?
Met de eenheidscirkel vind je (in ieder geval) twee antwoorden:

Dus $\alpha=\frac{1}{4}\pi$ of $\alpha=\frac{3}{4}\pi$. Maar klopt dat wel?
Nee, dat klopt niet. Er zijn oneindig veel oplossingen. $\alpha=2\frac{1}{4}\pi$ of $\alpha=2\frac{3}{4}\pi$ of $\alpha=4\frac{1}{4}\pi$ of $\alpha=4\frac{3}{4}\pi$, enz... maar ook $\alpha=-1\frac{1}{4}\pi$ of $\alpha=-1\frac{3}{4}\pi$.
Wij noemen dat wel modulo 2$\pi$. Dat wil zeggen dat er bij een oplossing bij steeds stapjes 2$\pi$ groter of kleiner ook oplossingen zijn.
Om alle antwoorden te geven gebruiken we de notatie $...+k\cdot2\pi$. Voor k kan je dan elk willekeurig geheel getal in vullen. Een oplossing zit er dan zo uit:
$\sin{\alpha}=\frac{1}{2}\sqrt{2}$
$\alpha=\frac{1}{4}\pi+k\cdot2\pi$ of $\alpha=\frac{3}{4}\pi+k\cdot2\pi$
Je hebt (in dit geval) dus twee verschillende verzamelingen van een oneindig aantal antwoorden.
$
\sin 2\alpha = \frac{1}{2}
$
$
2\alpha = \frac{1}{6}\pi + k \cdot 2\pi
$ of $
2\alpha = \frac{5}{6}\pi + k \cdot 2\pi
$
$
\alpha = \frac{1}{{12}}\pi + k \cdot \pi
$ of $
\alpha = \frac{5}{{12}}\pi + k \cdot \pi
$
De hoeken zoek je op in de eenheidscirkel en dan modulo $2\pi$. Daarna kan je de vergelijking verder oplossen. In dit geval deel je door $2$. Kijk maar 's goed!
$
\sin \left( {\frac{1}{2}\alpha - \frac{1}{2}\pi } \right) = - \frac{1}{2}\sqrt 3
$
$
\frac{1}{2}\alpha - \frac{1}{2}\pi = 1\frac{1}{3}\pi + k \cdot 2\pi
$ of $
\frac{1}{2}\alpha - \frac{1}{2}\pi = 1\frac{2}{3}\pi + k \cdot 2\pi
$
$
\frac{1}{2}\alpha = 1\frac{5}{6}\pi + k \cdot 2\pi
$ of $
\frac{1}{2}\alpha = 2\frac{1}{6}\pi + k \cdot 2\pi
$
$
\alpha = 3\frac{2}{3}\pi + k \cdot 4\pi
$ of $
\alpha = 4\frac{1}{3}\pi + k \cdot 4\pi
$
De hoeken zoek je op in de eenheidscirkel en dan modulo $2\pi$. Daarna kan je de vergelijking verder oplossen. In dit geval links en rechts $\frac{1}{2}\pi$ optellen en vermengvuldigen met $2$. Kijk maar weer 's goed!