|
Een experiment twee of meer keer uitvoeren
Bij het vaker uitvoeren van hetzelfde kansexperiment bereken je kansen met de productregel voor anafhankelijke gebeurtenissen.
Voorbeeld 1
Timo wil zo vaak met twee dobbelstenen gooien zodat de kans op minstens één keer 'som van de ogen is 12' groter is dan $\frac{3}{4}$.
-
Bereken hoe vaak Timo minstens moet gooien.
Uitwerking
-
$P(X \ge 1) = 1 - \left( {\frac{{35}}{{36}}} \right)^n$
Bovendien moet gelden:
-
$P(X \ge 1) > \frac{3}{4}$
Dat geeft:
-
$1 - \left( {\frac{{35}}{{36}}} \right)^n > \frac{3}{4}$
Oplossen geeft: $
n \ge 50
$
|
De algemene productregel
Voor de gebeurtenissen $A$ en $B$ geldt:
$
P(A \cap B) = P(A) \cdot P(B|A) = P(B) \cdot P(A|B)
$
Bij het pakken van knikkers uit een vaas gebruik je de algemene productregel voor het berekenen van kansen.
Voorbeeld 2
In een vaas zitten 8 witte, 4 blauwe en 2 rode ballen. We trekken steeds drie ballen uit de vaas zonder terugleggen.
-
Bereken de kans op 2 witte ballen.
Eén vraag drie uitwerkingen
1e manier
Aantal gunstige uitkomsten is 3·8·7·6=1008
Aantal mogelijke uitkomsten is 14·13·12=2184
$P({\rm{2}}\,\,{\rm{witte}})$=$\large\frac{1008}{2184}=\frac{6}{13}$
2e manier
$P(w,w,n)$ = $\large\frac{8}{14}\cdot\frac{7}{13}\cdot\frac{6}{12}=\frac{2}{13}$
$
P({\rm{2}}\,\,{\rm{witte}}) = 3 \cdot \frac{8}{{14}} \cdot \frac{7}{{13}} \cdot \frac{6}{{12}} = \frac{6}{{13}}
$
3e manier
$P({\rm{2}}\,\,{\rm{witte}})=$ $\Large\frac{{8\choose2}\cdot{6\choose1}}{{14\choose3}}$ $=\frac{6}{13}$
Zie één vraag drie uitwerkingen
|
|
Experimenten herhalen totdat succes optreedt
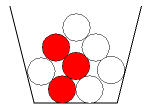
Je pakt één voor één knikkers uit een vaas met 3 rode en 5 witte knikkers. Je gaat net zo lang door tot je een rode knikkers pakt.
-
Wat is de kans dat je 4 keer een knikker moet pakken?
Uitgewerkt
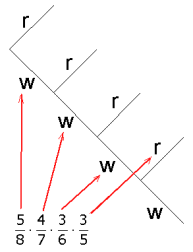
De eerste knikkers is wit, de tweede knikker is wit, de derde knikker is wit maar de vierde knikker is rood.
$
P(X = 4) = \frac{5}{8} \times \frac{4}{7} \times \frac{3}{6} \times \frac{3}{5} = \frac{3}{{28}}
$
|
Voorbeeld 3
In een vaas zitten 2 rode, 4 witte en 3 blauwe knikkers. Joris pakt één voor één knikkers uit de vaas. Hij gaat daar mee door totdat hij een blauwe knikker heeft.
Bereken, op 3 decimalen nauwkeurig, de kans dat Joris:
-
4 knikkers pakt
-
minstens 4 knikkers pakt
-
minder dan 4 knikkers pakt
Antwoorden
-
$P(X = 4) = \frac{6}{9} \times \frac{5}{8} \times \frac{4}{7} \times \frac{3}{6} \approx 0,119$
-
$P(X \ge 4) = \frac{6}{9} \times \frac{5}{8} \times \frac{4}{7} \approx 0,238$
-
$P(X < 4) \approx 1 - 0,238 = 0,762$
Met terugleggen
Dezelfde vragen, maar dan met met terugleggen:
-
$
P(x = 4) = \left( {\frac{6}{9}} \right)^3\cdot \frac{3}{9} \approx 0,099
$
-
$
P(X \ge 4) = \left( {\frac{6}{9}} \right)^3\approx 0,296
$
-
$
P(X < 4) = 1 - 0,296 = 0,704
$
|