opdracht 1 en 2 uitgewerkt

Opdracht 1 Gegeven: $BE=3$, $AE=2$ en $EF=2$ Gevraagd: bereken $\angle C$ in hele graden.

Opdracht 2 Gegeven: $BC=5$, $EF=3$ en $EB=2$. Gevraagd: bereken $\angle A$ in hele graden.

$\Delta ABC \sim \Delta FBE$, want: $\angle A=\angle BFE$ (rechte hoek) $\angle B=\angle B$ (triviaal) Twee driehoeken met twee gelijke hoeken dus $\Delta ABC \sim \Delta FBE$. $\angle C=\angle FEB$. In $\Delta BFE$ kan je $\angle FEB$ uitrekenen met de cosinus. $cos(\angle FEB)=\frac{2}{3}$ $\angle FEB\approx48^o$

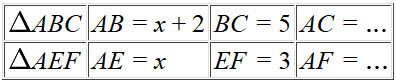
$\Delta ABC \sim \Delta AEF$, want: $\angle A=\angle A$ (triviaal) $\angle AEF=\angle ABC$ (rechte hoek) Kies $AE=x$ en vul de verhouidingstabel in: Met kruislings vermenigvuldigen krijg je: $3(x+2)=5x$ $3x+6=5x$ $2x=6$ $x=3$ Als $AE=3$ en $EF=3$ dan $\angle A=45^o$