
Oplossing week 17
Oplossing 1
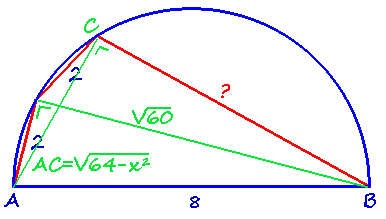
Met de stelling van Ptolemaeus geeft dat:
$ \eqalign{ & \sqrt {60} \cdot \sqrt {64 - x^2 } = 2 \cdot 8 + 2x \cr & \sqrt {3840 - 60x^2 } = 2x + 16 \cr & 3840 - 60x^2 = 4x^2 + 64x + 256 \cr & 64x^2 + 64x - 3584 = 0 \cr & x^2 + x - 56 = 0 \cr & (x + 8)(x - 7) = 0 \cr & x = - 8\,\,(v.n.)\,\, \vee x = 7 \cr & x = 7 \cr} $
Maar dat kan vast ook anders...
Oplossing 2
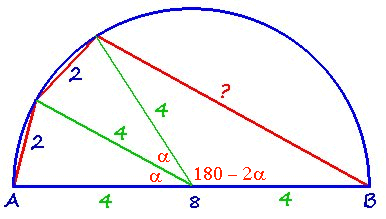
Gebruik de cosinusregel:
$
\eqalign{
& 2^2 = 4^2 + 4^2 - 2 \cdot 4 \cdot 4 \cdot \cos \alpha \cr
& \cos \alpha = \frac{7}
{8} \cr
& \cos 2\alpha = 2\cos ^2 \alpha - 1 \cr
& \cos 2\alpha = \frac{{17}}
{{32}} \cr}
$
Nogmaals de cosinusregel:
$
\eqalign{
& x^2 = 16 + 16 - 2 \cdot 4 \cdot 4 \cdot \cos (180 - 2\alpha ) \cr
& x^2 = 32 - 32 \cdot - \frac{{17}}
{{32}} \cr
& x^2 = 49 \cr
& x = 7 \cr}
$
Ook mooi...
Oplossing 3
Met dank aan Erik:
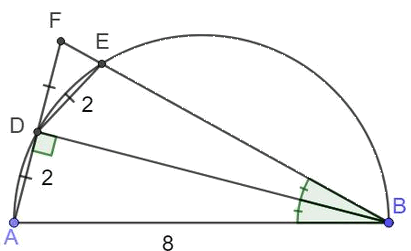




©2004-2025 Wiskundeleraar - login
|