|
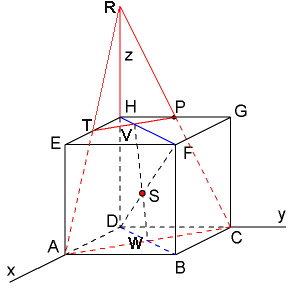
Stel een vectorvoorstelling op van het vlak $V$ door $APC$ en stel een vectorvoorstelling op van de lijn $k$ door $DF$. Je kunt dan vrij eenvoudig het snijpunt $S$ berekenen:
$ \begin{array}{l} \left. \begin{array}{l} V:\left( {\begin{array}{*{20}c} x\\ y\\ z\\ \end{array}} \right) = \left( {\begin{array}{*{20}c} 4\\ 0\\ 0\\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c} {-1}\\ 1 \\ 0\\ \end{array}} \right) + \mu \left( {\begin{array}{*{20}c} {-1}\\ 0\\ 2\\ \end{array}} \right) \\ k:\left( {\begin{array}{*{20}c} x\\ y\\ z\\ \end{array}} \right) = \rho \left( {\begin{array}{*{20}c} 1\\ 1\\ 1\\ \end{array}} \right) \\ \end{array} \right\} \Rightarrow \\ \left\{ \begin{array}{l} 4 - \lambda - \mu = \rho \\ \lambda = \rho \\ 2\mu = \rho \\ \end{array} \right. \\ \left\{ \begin{array}{l} 4 - \lambda - \mu = \rho \\ \lambda = \rho \\ \mu = \frac{1}{2}\rho \\ \end{array} \right. \\ 4 - \rho - \frac{1}{2}\rho = \rho \\ 2\frac{1}{2}\rho = 4 \\ \rho = 1\frac{3}{5} \\ S\left( {1\frac{3}{5},1\frac{3}{5},1\frac{3}{5}} \right) \\ \end{array} $
Dat is toch wel bijzonder. Geen wortels, geen gelijkvormigheid, maar wel opgelost...:-)
|