|
Hoe vaak moet je met een dobbelsteen gooien zodat de kans op minstens vier keer zes ogen te gooien groter is dan $0,95$?
$X$~binomiaal verdeeld
$p=\frac{1}{6}$
$n=?$
$P(X\ge 4)>0,95$
Er geldt: $1-P(X\le 3)>0,95$. Om $n$ te berekenen gebruik je het Table-menu van je GR.
|
 |
|
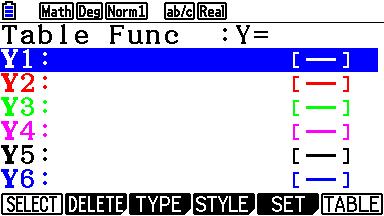
We gaan nu bij $Y1$ deze formule invoeren:
Y1=1-BinomialCD(3,x,$\frac{1}{6}$)
De functie BinomialCD() kan je vinden via OPTN.
|
 |
|
De functie BinomialCD() kan je vinden via OPTN, [>], STAT, DIST, BINOMIAL en Bcd.
|
 |
|
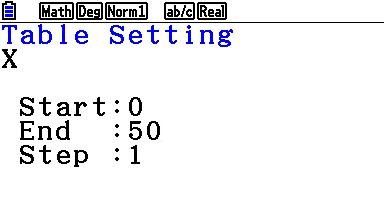
Met SET moet je dan de tabel instellen. |
 |
|
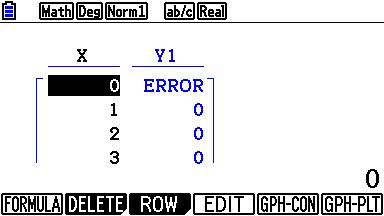
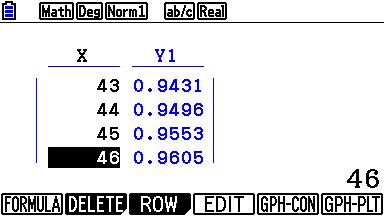
Tik TABLE en je krijgt een tabel met de kansen voor verschillende waarden van $n$. Blader in de tabel om te zien wanneer de kans voor het eerst groter is dan $0,95$ |
 |
|
Het blijkt dat de kans voor 't eerst groter is dan $0,95$ bij $n=45$.
ANTWOORD
Je moet 45 keer met een dobbelsteen gooien zodat de kans op minstens vier keer zes ogen te gooien groter is dan $0,95$
|
 |
|