|
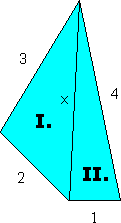
Formule van Heron I. $\eqalign{O^{2}_{I.}=\frac{(1-x^{2})(x^{2}-25)}{16}}$ II. $\eqalign{O^{2}_{II.}=\frac{(9-x^{2})(x^{2}-25)}{16}}$ Neem u=x² en A als de totale oppervlakte van de vierhoek. Dan geldt: $\eqalign{A=\frac{1}{4}\sqrt{(1-u)(u-25)}+\frac{1}{4}\sqrt{(9-u)(u-25)}}$ $A'=0$ voor $u=15\frac{2}{5}$ en dat geeft $A=2\sqrt{6}$ Opgelost...:-)
|