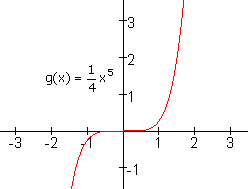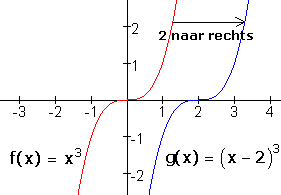Machtsfunctie

Een machtsfunctie $f$ heeft de vorm:

  • $f(x)=ax^n$

Grafieken van machtsfuncties

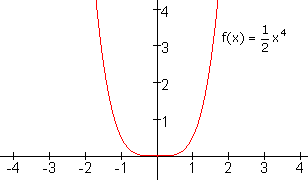
q6882img1.gif

  • Als n even is dan is de grafiek symmetrisch met de y-as als symmetrie-as.

Grafieken van machtsfuncties

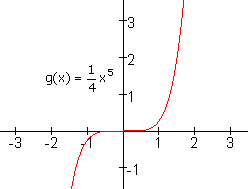
q6882img2.gif

  • Als n oneven is dan is de grafiek puntsymmetrisch met O(0,0) als punt van symmetrie.

Grafieken en aantal oplossingen

Als je kijkt naar vergelijkingen van de vorm $x^n=a$ dan kan je op basis van de grafiek van een machtsfunctie besluiten of je geen, één of twee oplossingen hebt.

n is even
a$>$0

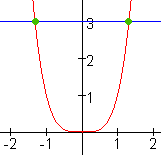
q6883img1.gif


2 oplossingen

n is oneven
a$>$0

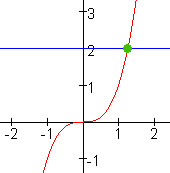
q6883img3.gif

1 oplossing

n is even
a$<$0

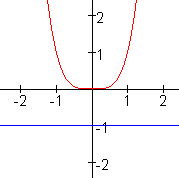
q6883img2.gif

geen oplossing

n is oneven
a$<$0

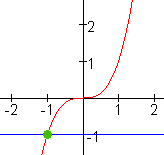
q6883img4.gif


1 oplossing

Voorbeelden

$
\eqalign{
&x^6=80\cr
&x=\root6\of{80}\vee x=-\root6\of{80}\cr
&x\approx2,08\vee x\approx-2,08\cr}
$		 $
\eqalign{
&2x^7=20\cr
&x^7=10\cr
&x=\root7\of{10}\approx1,39\cr}
$		 $
\eqalign{
&4x^{10}+10=6\cr
&4x^{10}=-4\cr
&x^{10}=-1\cr}
$
geen oplossing		 $
\eqalign{
&\frac{2}
{3}x^3=-2\cr
&x^3=-6\cr
&x=\root3\of{-6}\approx-1,82\cr}
$

Opgave 9

Los exact op:

  1. $4{x^4} = 20$
  2. $4{x^5} - 20 = 0$
  3. ${x^6} = \pi$
  4. $32{x^6} + 19 = 1$
Transformaties van machtsfuncties

Je kunt op grafieken allerlei transformaties uitvoeren:

  • naar links of rechts verschuiven
  • naar onderen of naar boven verschuiven
  • vermenigvuldigen met een factor ten opzichte van de x-as.

Op de volgende bladzijde zie je daar voorbeelden van.

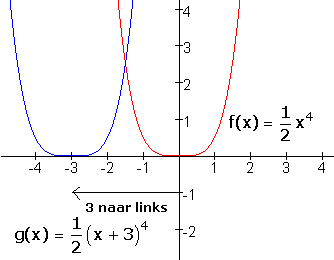
q6900img1.gif

3 naar links verschuiven
vervang 'x' door 'x+3'

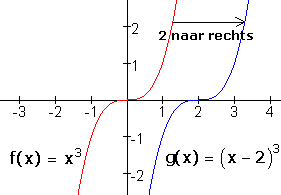
q6900img2.gif

2 naar rechts verschuiven
vervang 'x' door 'x-2'

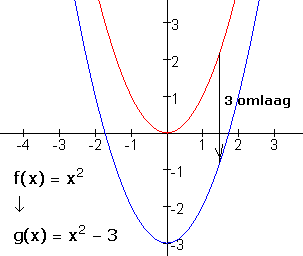
q6900img3.gif

3 omlaag verschuiven
trek er 3 van af

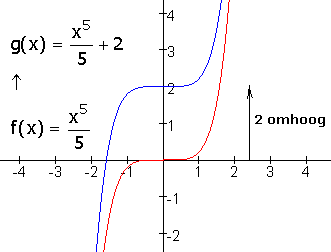
q6900img4.gif

2 omhoog verschuiven
tel er 2 bij op

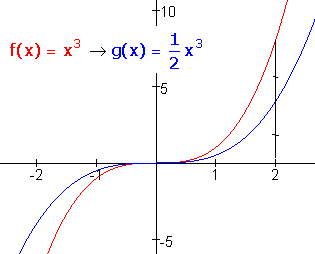
q6900img5.gif

vermenigvuldigen met een factor $
\frac{1}
{2}
$
alles wordt de helft

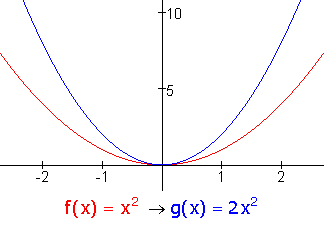
q6900img6.gif

vermenigvuldigen met een factor 2
alles wordt 2 keer zo groot

Opdracht
  • Start het online grafiekenprogramma op.
    Je kunt een link vinden naar het programma op wiskundeleraar.nl bij de hulpmiddelen of type https://www.desmos.com/calculator in de adresbalk van je browser.

Opgave 10

  • Welke transformaties moet je toepassen op $y=x^4$ om de functie $y=-2(x+3)^4+5$ te krijgen?
    Controleer je antwoord met het grafiekenprogramma

Opgave 11

Je past achtereenvolgens de volgende transformatie toe op $y=x^5$ om de functie $g$ te krijgen:

translatie over de vector $(2, 0)$
vermenigvuldigen met de factor $\frac{1}{2}$ t.o.v. de $x$-as
translatie over vector $(0, -3)$

  • Geef een functievoorschrift van $g$.
    Controleer je antwoord met het grafiekenprogramma

Opgave 12

  • Onderzoek of de volgorde van de transformaties bij opgave 11 van belang is.