|
Opdracht
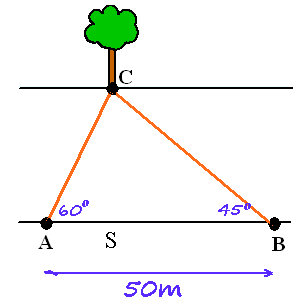
Ik sta aan de oever van een brede rivier en wil graag de breedte ervan bepalen. Gelukkig staat er een boom aan de overkant.
Ik zoek twee punten $A$ en $B$ zodat de hoeken die de oever maakt met de lijn naar de voet $C$ van de boom gelijk zijn aan $\angle ABC=45°$ en $\angle BAC=60°$.
Ik meet de afstand AB. Deze afstand is gelijk aan 50 meter.
-
Bereken exact de breedte van de rivier?

|
Uitwerking
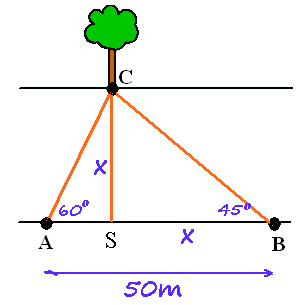
In $\Delta$ASC geldt $\eqalign{\frac{AS}{CS}=\frac{1}{\sqrt{3}}=\frac{50-x}{x}}$.
Kruislings vermenigvuldigen en oplossen geeft:
$
\eqalign{
& x = \sqrt 3 \cdot \left( {50 - x} \right) \cr
& x^2 = 3 \cdot \left( {50 - x} \right)^2 \cr
& x^2 = 3\left( {2500 - 100x + x^2 } \right) \cr
& x^2 = 7500 - 300x + 3x^2 \cr
& 2x^2 - 300x + 7500 = 0 \cr
& x^2 - 150x + 3750 = 0 \cr
& (x - 75)^2 - {\text{5625 + 3750 = 0}} \cr
& (x - 75)^2 - {\text{1875 = 0}} \cr
& (x - 75)^2 = {\text{1875}} \cr
& x - 75 = - 25\sqrt {\text{3}} \vee x - 75 = 25\sqrt {\text{3}} \cr
& x = 75 - 25\sqrt {\text{3}} \vee x = 75 + 25\sqrt {\text{3}} \,\,(v.n.) \cr
& x = 75 - 25\sqrt {\text{3}} \cr}
$
|