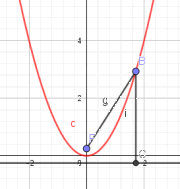
De parabool met brandpunt $F(0,\frac{1}{2}p)$ en richtlijn $l:y=-\frac{1}{2}p$ heeft vergelijking $x^2=2py$.
Je kunt $(x-a)^2=2p(y-b)$ beschouwen als een translatie over de vector $ \left( {\begin{array}{*{20}c}
   a  \\
   b  \\
\end{array}} \right)
$ van $x^2=2py$. Er geldt:

• Top $(a,b)$
• Brandpunt $F(a,\frac{1}{2}p+b)$
• Richtlijn $l:y=-\frac{1}{2}p+b$

Voorbeeld

Gegeven: $x^2  + 4y = 6 - 3x$

• Geef de coördinaten van het brandpunt en een vergelijking van de richtlijn.

Uitgewerkt

$
\eqalign{
  & x^2  + 4y = 6 - 3x  \cr
  & x^2  + 3x =  - 4y + 6  \cr
  & \left( {x + \frac{3}
{2}} \right)^2  - 2\frac{1}
{4} =  - 4y + 6  \cr
  & \left( {x + \frac{3}
{2}} \right)^2  =  - 4y + \frac{{33}}
{{4}}  \cr
  & \left( {x + \frac{3}
{2}} \right)^2  =  - 4\left( {y - \frac{{33}}
{{16}}} \right) \cr}
$

Dus $p=-2$ en Top$(-1\frac{1}{2},2\frac{1}{16})$

• Brandpunt $F(-1\frac{1}{2},1\frac{1}{16})$
• Richtlijn $l:y=-3\frac{1}{16}$

Zie Re: Brandpunt parabool