Wetenschappelijke notatie

Grote getallen zijn vaak lastig te lezen. Hoeveel is bijvoorbeeld 23000000000000?
Eén manier om het lezen te vergemakkelijken is het zetten van puntjes of spaties:
23.000.000.000.000 of 23 000 000 000 000.

Kleine getallen zijn ook lastig om te lezen. Wat staat hier precies?
0,000000000000000003

Het is handiger om grote en kleine getallen te schrijven al getallen keer een macht van 10.

$3,2\times 10^{12}$ = $3.200.000.000.000$

$3\times 10^{-20}$ = $0,00000000000000000003$

Handig toch?

Lengte, oppervlakte en inhoud

Hieronder staan de belangrijke maten voor lengte, oppervlakte en inhoud.

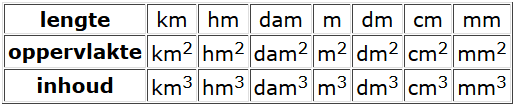
• Bij de lengtematen zit er tussen elke stap een factor 10
• Bij de oppervlaktematen zit er tussen elke stap een factor 100
• Bij de inhoudsmaten zit er tussen elke stap een factor 1000

Verder is 1L=10dL=100cL=1000mL. Onthouden: 1L=1dm³.

$
\eqalign{{\rm{snelheid = }}{{{\rm{afstand}}} \over {{\rm{tijd}}}}}
$
Er zijn nu allerlei mogelijkheden. Als je de afstand en de tijd weet dan kan je snelheid uitrekenen. Als je de snelheid weet en de afstand dan kan je de tijd uitrekenen. Als je tijd en de snelheid weet dan kan je de afstand uitrekenen.

• Vul de formule in voor zover je weet wat je hebt en gebruik de breuk om te bedenken wat je moet doen...

Omrekenen van m/s naar km/h en andersom

Af en toe moet je snelheden omrekenen van meters per seconde naar kilometers per uur of andersom. Daar was een 'truuk' voor:

$
\large\frac{{meter}}
{{seconde}} \to \times 3,6 \to \frac{{kilometer}}
{{uur}}
$

$
\large\frac{{kilometer}}
{{uur}} \to :3,6 \to \frac{{meter}}
{{seconde}}
$

Maar waar komt dat vandaan? Wat moet je doen als je vergeten bent hoe dat precies zat?

Dan maar liever zo:

• 15 km/uur = 15.000 m/uur = $\large\frac{15.000}{3.600}$ m/s $\approx$ 4,17 m/s
• 6 m/s = 6·3600 m/uur = 21.600 m/uur = 21,6 km/uur

1 uur = 3600 seconden
1 kilometer = 1000 meter

Omrekenen van tijd in uren naar uren, minuten en seconden en andersom

Sommige mensen denken dat 4:25 uur gelijk is aan 4,25 uur, maar dat klopt niet. 4:25 uur is gelijk aan 4 uur en 25 minuten en dat is gelijk aan 4+$\frac{25}{60}$ uur $\approx$ 4,416 uur.

Andersom is 4,15 uur niet gelijk aan 4 uur en 15 minuten. 4,15 uur is gelijk aan 4 uur en $\frac{15}{100}$×60=9 minuten.

Voorbeeld

• Johan doet over een afstand van 25 km 3 uur, 20 minuten en 30 seconden. Wat is zijn gemiddelde snelheid in km/h?

Ik zou graag de afstand (in km) willen delen door de tijd (in uren). Dan krijg je de snelheid in kilometer per uur. Ik moet die 3:20:30 schrijven als een decimaal getal.

3:20:30=3+$\frac{20}{60}$+$\frac{30}{3600}$ uur $\approx$ 3,342 uur.

De gemiddelde snelheid is $\frac{25}{3,342}\approx7,48$ km/h