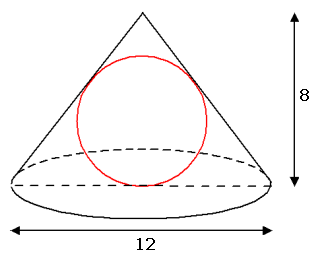
Gegeven is een kegel met een diameter van het grondvlak van 12 en een hoogte van 8. In de kegel past precies een bol.

Je wilt dan de straal van de bol weten. Maak een tekening:
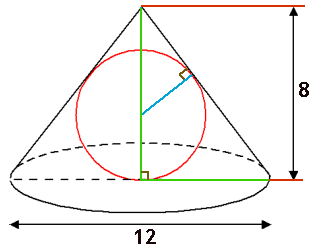
De straal is $r$. Je krijgt dan:
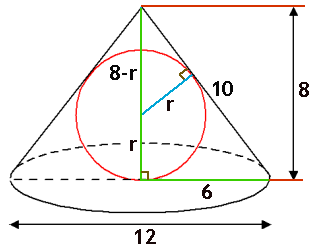
Gelijkvormigheid
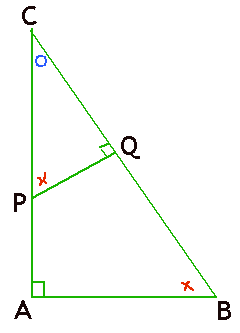
Driehoek ABC is gelijkvormig met driehoek PQC, kijk naar de overeenkomstige hoeken.
$\angle$A is gelijk aan $\angle$Q, want die zijn beide 90$^o$.
$\angle$C is gelijk aan $\angle$C (triviaal:-)
$\angle$B is gelijk aan $\angle$P, want de som van de hoeken is 180$^o$
$\Delta$ABC~$\Delta$QPC
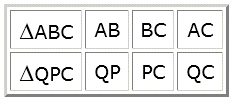
Invullen:
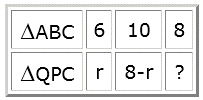
Kruislings vermenigvuldigen geeft:
$\begin{array}{l} 6(8 - r) = 10 \cdot r \\ 48 - 6r = 10r \\ 16r = 48 \\ r = 3 \\ \end{array} $
Oppervlakte en inhoud
$
\begin{array}{l}
O_{kegel} = \pi r^2 + \pi rR = \pi \cdot 6^2 + \pi \cdot 6 \cdot 10 = 96\pi \\
I_{kegel} = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi \cdot 6^2 \cdot 8 = 96\pi \\
O_{bol} = 4\pi r^2 = 4\pi \cdot 3^2 = 36\pi \\
I_{bol} = \frac{4}{3}\pi r^3 = \frac{4}{3}\pi \cdot 3^3 = 36\pi \\
\end{array}
$