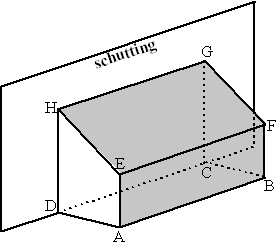
 Met behulp van een frame van uitschuifbare tentstokken AE en BF en een rechthoekig zeil van 5 bij 10 meter wordt tegen een schutting een opslagruimte gemaakt in de vorm van een recht prisma AEHD.BFGC.
Met behulp van een frame van uitschuifbare tentstokken AE en BF en een rechthoekig zeil van 5 bij 10 meter wordt tegen een schutting een opslagruimte gemaakt in de vorm van een recht prisma AEHD.BFGC.
 Met behulp van een frame van uitschuifbare tentstokken AE en BF en een rechthoekig zeil van 5 bij 10 meter wordt tegen een schutting een opslagruimte gemaakt in de vorm van een recht prisma AEHD.BFGC.
Met behulp van een frame van uitschuifbare tentstokken AE en BF en een rechthoekig zeil van 5 bij 10 meter wordt tegen een schutting een opslagruimte gemaakt in de vorm van een recht prisma AEHD.BFGC.
De grensvlakken AEHD en BFGC blijven open en hebben elk de vorm van een trapezium met rechte hoeken in A, D, B en C.
De breedte AD van de opslagruimte is 3 meter. Het zeil wordt met de lange kant van 10 meter op de grond bevestigd langs AB.
Het zeil wordt over de stok EF strak gespannen naar de schutting waar het zo hoog mogelijk wordt bevestigd. In de figuur is dat langs HG.
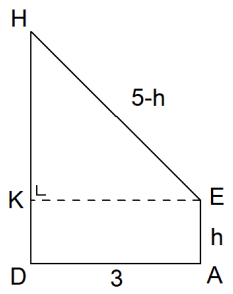
De korte kant van het zeil valt langs AE en EH. AE + EH = 5 meter. Doordat AE (= BF) variabel is, zal de hoogte van HG ook variabel zijn. De inhoud V van het prisma AEHD.BFGC hangt af van de lengte h van AE.
$
\eqalign{
& AE = 1 \cr
& HE = 5 - h \cr
& KH^2 = \left( {5 - h} \right)^2 - 9 \cr
& KH = \sqrt {16 - 10h + h^2 } \cr
& O(AEHD) = O(AEKH) + O(\Delta KEH) \cr
& O(AEHD) = 3 \cdot h + \frac{1}
{2} \cdot 3 \cdot \sqrt {16 - 10h + h^2 } \cr
& V = 10\left( {3h + 1\frac{1}
{2}\sqrt {16 - 10h + h^2 } } \right) \cr
& V = 30h + 15\sqrt {16 - 10h + h^2 } \cr}
$
Dit is een goed voorbeeld van een opgave waarbij, als het opstellen van een formule lastig is, een concreet voorbeeld goed kan helpen. Neem bijvoorbeeld $h=1$ en bereken de inhoud. Je krijgt:

$
\eqalign{
& Neem\,\,h = 1 \cr
& AE = 1 \cr
& HE = 5 - 1 = 4 \cr
& KH^2 = 4^2 - 9 = 16 - 9 = 7 \cr
& KH = \sqrt 7 \cr
& O(AEHD) = O(AEKH) + O(\Delta KEH) \cr
& O(AEHD) = 3 \cdot 1 + \frac{1}
{2} \cdot 3 \cdot \sqrt 7 \cr
& V = 10\left( {3 + 1\frac{1}
{2}\sqrt 7 } \right) \cr
& V = 30 + 15\sqrt 7 \cr}
$
Neem dan $h$ en doe dezelfde procedure nog een keer en dan zou de formule er als vanzelf uit moeten rollen.
Een belangrijk punt om te maken is dat het rekenen met variabelen niet anders is dan het rekenen met getallen. Sterker nog: in deze hoedanigheid is de variabele $h$ een getal. Het is weliswaar een (nog) onbekend getal. Als je 't hebt over getalsvariabelen dan zou je met de kennis van het 'normale rekenen' ook moeten kunnen rekenen met varabelen. Ik kan nog wel een keer benadrukken dat daarvoor een goede rekenvaardigheid van groot belang is.
Vandaar dat het een goede oefening is om bij het maken van formules te bedenken dat het hier om getallen gaat. Neem 's een concreet getal voordat je aan de formules begint. Deze opgave is daar een mooi voorbeeld van.