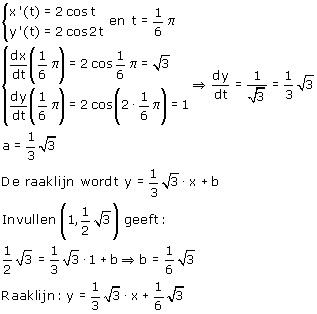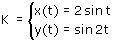
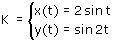
Voor punten waar de raaklijn aan de kromme horizontaal is moet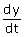 
=0 en 
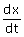$\ne$0 zijn. Je kunt ook zeggen dat de verticale snelheid in zo'n punt gelijk aan nul is.
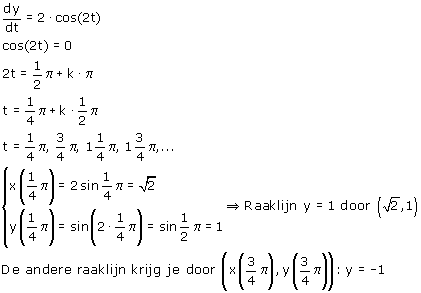
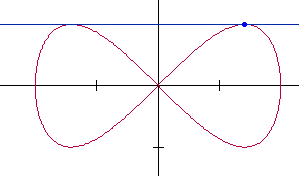
Voor punten waar de raaklijn verticaal is geldt: 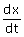=0 en 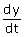$\ne$0. Je kan ook zeggen dat de horizontale snelheid gelijk aan nul is.
De vergelijking van een willekeurige raaklijn aan de kromme is gelijk aan y=ax+b. Hierin in a de richtingscoëfficiënt en (0,b) het snijpunt met de y-as.
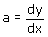
Voor een willekeurig punt van de kromme is de richtingscoëfficiënt van de raaklijn gelijk aan:
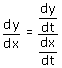
De waarden va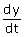n en 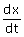in het punt kan je bepalen. Met het invullen van het raakpunt kan je dan ook b bepalen.
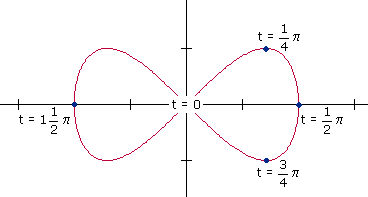
Voorbeeld
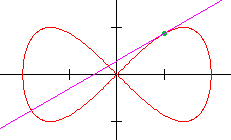
Geef de vergelijking van de raaklijn aan de kromme in het punt (1,$\frac{1}{2}\sqrt{3}$).
Uitwerking
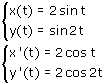
Maar wat is nu de waarde van t?
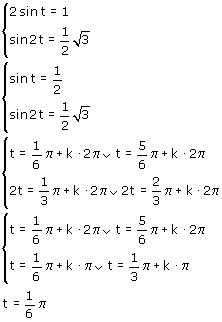
Nu kan je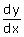 
berekenen:
