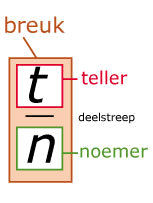
Om breuken op te tellen of af te trekken maak je de breuken gelijknamig. Gelijknamig maken wil zeggen dat je zorgt voor 'gelijke noemers':
$
\eqalign{\frac{1}{3} + \frac{2}{5} = \frac{5}{{15}} + \frac{6}{{15}} = \frac{{11}}{{15}}}
$
Om de breuken met 'derden' en 'vijfden' gelijknamig te maken kan je als noemer '3×5' nemen. Soms kan het met een kleiner getal.
$
\eqalign{\frac{1}{3} + \frac{7}{{12}} = \frac{4}{{12}} + \frac{7}{{12}} = \frac{{11}}{{12}}}
$
Je gebruikt bij het gelijknamig maken de rekenregel dat je teller en noemer met hetzelfde getal mag vermenigvuldigen of delen. De waarde van de breuk blijft dan hetzelfde. Je gebruikt deze regel ook bij het vereenvoudigen van breuken.
$
\eqalign{\frac{1}{4} + \frac{5}{{12}} = \frac{3}{{12}} + \frac{5}{{12}} = \frac{8}{{12}} = \frac{2}{3}}
$
Je kunt breuken ook van elkaar aftrekken:
$
\eqalign{\frac{5}{6} - \frac{1}{4} = \frac{{10}}{{12}} - \frac{3}{{12}} = \frac{7}{{12}}}
$
Optellen en aftrekken van samengestelde breuken
$
\eqalign{2\frac{3}{5} + 1\frac{1}{4} = 2\frac{{12}}{{20}} + 1\frac{5}{{20}} = 3\frac{{17}}{{20}}}
$
$
\eqalign{2\frac{3}{5} - 1\frac{1}{4} = 2\frac{{12}}{{20}} - 1\frac{5}{{20}} = 1\frac{7}{{20}}}
$
Soms moet je bij optellen nog de helen uithalen:
$
\eqalign{5\frac{4}{5} + 1\frac{3}{4} = 5\frac{{16}}{{20}} + 1\frac{{15}}{{20}} = 6\frac{{31}}{{20}} = 7\frac{{11}}{{20}}}
$
Soms moet je bij aftrekken lenen:
$
\eqalign{7\frac{1}{5} - 1\frac{3}{4} = 7\frac{4}{{20}} - 1\frac{{15}}{{20}}}
$
Lenen...!
$
\eqalign{7\frac{4}{{20}} - 1\frac{{15}}{{20}}=6\frac{{24}}{{20}} - 1\frac{{15}}{{20}} = 5\frac{9}{{20}}}
$