Een annuïteit is een vast bedrag dat periodiek betaald of ontvangen wordt gedurende een bepaalde periode. Letterlijk genomen is een annuïteit een jaarlijks te betalen bedrag. Het is afgeleid van het Latijnse woord "annus" (jaar). Het woord 'annuïteit' wordt in Nederland echter heel algemeen gebruikt voor een periodiek bedrag, ook bij een andere periode dan een jaar, vaak een maand. De periode moet er dus wel bij vermeld worden, ook als de periode een jaar betreft.
@wikipedia
|
Opgave
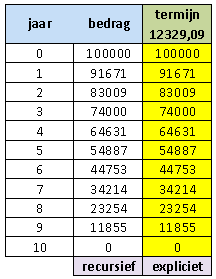
Een bedrag van €100.000,- wordt geleend tegen een jaarrente van 4%. Het bedrag moet worden terugbetaald in 10 jaar.
-
Bereken het termijnbedrag per jaar.
-
Geef de expliciete formule.
Uitwerking
De directe formule van $u_n=a\cdot u_{n-1}+b$ is:
-
$u_n=A\cdot a^n+\overline u$
Waarij $\overline u$ het dekpunt is en $A$ een constante.
Aanpak
-
Bereken het dekpunt
-
Gebruik de startwaarde om $A$ te berekenen.
Stap 1
-
Voor het dekpunt $\overline u$ geldt $1,04^{10}\cdot(\overline u-100.000)=\overline u$
-
Oplossen geeft $\overline u\approx308227,36$
-
De aflossingstermijn is $0,04\cdot308227,36\approx12329,09$
Stap 2
-
Vul in de formule $u_n=A\cdot1,04^n+308227,36$ in dat $u_{10}=0$
-
Dat geeft $0=A\cdot1,04^{10}+308227,36$
-
Zodat $A\approx-208227,36$
-
De expliciete formule is dan $u_n=-208227,36\cdot1,04^n+308227,36$
|