Oplossing week 6
De oplossing kan je vinden op de futility-website.
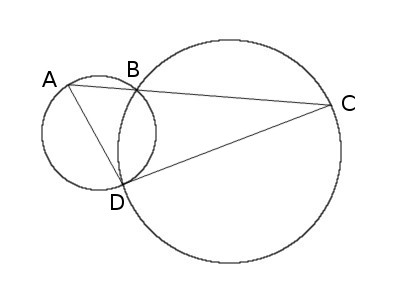
Call the other intersection point D and draw AD and DC. All angles inscribed in a circle and subtended by the same chord are equal, so angle BAD retains the same measure as A travels around its circle. Similarly, angle BCD remains the same as C travels around its circle. This means that triangle ADC will always have the same shape: As line AC pivots around B, triangle ADC will vary in size but remain self-similar.
So which position will maximize its size? AD and DC are chords of their respective circles, and the longest chord is a diameter. So turn the triangle until both of these lines are diameters (this will happen simultaneously); at that point triangle ADC will reach its maximum size and line AC its maximum length.
From Mogens Larsen in Richard Guy and Robert Woodrow, eds., The Lighter Side of Mathematics, 1994.