2. het binomium van Newton
De driehoek van Pascal
Elk getal in de driehoek van Pascal geeft het aantal kortste routes om vanuit de top op die plaats te komen.
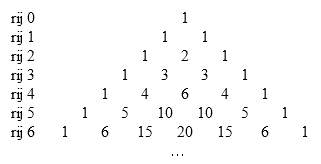
De getallen in de $n$-de rij zijn:
$
\left( {\begin{array}{*{20}c}
n\\
0\\
\end{array}} \right),\left( {\begin{array}{*{20}c}
n\\
1\\
\end{array}} \right),\left( {\begin{array}{*{20}c}
n\\
2\\
\end{array}} \right),...,\left( {\begin{array}{*{20}c}
n\\
n\\
\end{array}} \right)
$
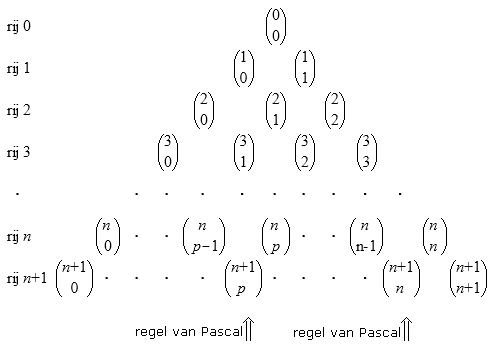
De som van de getallen in de $n$-de rij is $2^n$
De regel van Pascal
In de driehoek van Pascal is elk getal de som van de twee getallen die er schuin boven staan.
$
\left( {\begin{array}{*{20}c}
n\\
{k-1}\\
\end{array}} \right) + \left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
{n+1}\\
k\\
\end{array}} \right)
$
Sigma-notatie
Met het wiskundige symbool $\Sigma$ kunnen we (oneindige) reeksen kort opschrijven. De letter $\Sigma$ is de hoofdletter S uit het Griekse alfabet. Het symbool $\Sigma$ is een somteken (en heeft dus alles te maken met optellen):
De formule $
\sum\limits_{k = 1}^\infty {\frac{1}{{2^k }}}
$ staat voor de oneindige som $
\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...
$. Voor elk getal $
k = 1,\,\,2,\,\,3,\,\,...
$ tel je de breuken bij elkaar op.
$
\sum\limits_{k = 1}^5 k = 1 + 2 + 3 + 4 + 5 = 15
$
$
\sum\limits_{k = 0}^5 {\left( {\begin{array}{*{20}c}
5\\
k\\
\end{array}} \right) \cdot 2^k } = 3^5
$
$
\sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)} = 2^n
$
$
\sum\limits_{k = 1}^\infty {\frac{1}{{2^k }}} = 1
$

- Zie uitstapje
Binomiaalcoëfficiënten
Bij het herleiden van $(a+b)^n$ komen de getallen van de $n$-de rij van Pascal tevoorschijn.
In het algemeen geldt:
$
\left( {a + b} \right)^n = \sum\limits_{k = 0}^n {\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)} \cdot a^{n - k} \cdot b^k
$
Deze formule heet het binomium van Newton. De getallen $
{\left( {\begin{array}{*{20}c}
n\\
k\\
\end{array}} \right)}
$ heten binomiaalcoëfficiënten.
Voorbeeld 1
Laat zien dat:
$
(x - 2)^3 = x^3 - 6x^2 + 12x - 8
$
Zie uitwerking
Voorbeeld 2
Geef de coëfficiënt van de vijfde term in de uitwerking van $(2p-3q)^7$.
Antwoord
Bij de vijfde term is $k=4$. Je krijgt dan:
$
\left( {\begin{array}{*{20}c}
7\\
4\\
\end{array}} \right) \cdot \left( {2p} \right)^3\cdot \left( { - 3q} \right)^4
$
Uitwerken geeft:
$
22680p^3 q^4
$
Het antwoord is $22680$
Multinomiaalcoëfficiënten
De coëfficiënten in de herleiding van een mulitonomium heten multinomiaalcoëfficiënten.
In de herleiding van $(p+q+r)^7$ is de binomiaalcoëfficiënt van $p^4q^2r$ gelijk aan:
$\left( {\begin{array}{*{20}c}
7\\
{4,2,1}\\
\end{array}} \right) $ = $\Large\frac{{7!}}{{4! \cdot 2! \cdot 1!}}$
De herleiding van $(p+q+r)^7$ kan met de sigma-notatie worden geschreven als:
$
(p + q + r)^7 = \sum\limits_{i + j + k = 7}^{} {\left( {\begin{array}{*{20}c}
7\\
{i,j,k}\\
\end{array}} \right)}\cdot p^i q^j r^k
$
...en dat is aan de vage kant:-)
