K. Oppervlakte van ruimtefiguren
Opgave
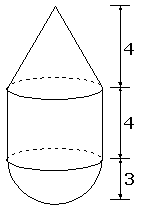
Dit object bestaat uit een kegel, cilinder en een halve bol.
- Bereken de oppervlakte op 1 decimaal nauwkeurig.
Uitwerking
Vanwege de halve bol weet je dat $r=3$.
Wat heb je nodig?
- Oppervlakte kegelmantel met $r=3$ en $R=5$
- Cilindermantel met $r=3$ en $h=4$
- Halve bol met $r=3$
$O_{totaal}=\pi rR+2\pi r·h+\frac{1}{2}·4\pi r^2$
$O_{totaal}=\pi·3·5+2\pi·3·4+\frac{1}{2}·4\pi·3^2$
$O_{totaal}=15\pi+24\pi+18\pi$
$O_{totaal}=57\pi$
$O_{totaal}\approx179,1$
Toelichting
- Het eerste probleem is om vast te stellen dat de straal $r$ van de bol, de grondcirkel van de cilinder en het grondcirkel van de kegel gelijk aan $3$ is. Dat lijkt 'nogal logisch' maar niet altijd voor iedereen.
- De formules op de formulekaart voor de oppervlakte van de cilinder en de kegel bestaan uit twee delen. De oppervlakte van de mantels en de oppervlakte van de cirkels. Maar wat is wat?
- Het is handig om bij de berekening $\pi$ zo lang mogelijk te laten staan en pas aan het eind af te ronden op 1 decimaal.
Begrip en inzicht
Uit het examenprogramma HAVO wiskunde B:
Domein C: Ruimtemeetkunde
-
Subdomein C1: Oppervlakte en inhoud
- De kandidaat kan de oppervlakte van vlakke en ruimtelijke figuren berekenen, van ruimtelijke figuren de inhoud berekenen en schatten en het effect van schaalvergroting op zowel inhoud als oppervlakte beargumenteren.
Het is handig te weten hoe de formules voor de ruimtefiguren in elkaar steken:
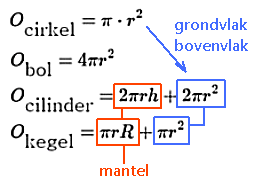
Leerlingen zouden in de formules de formule voor de oppervlakte van een cirkel moeten herkennen. De andere term moet dan wel de oppervlakte van de mantel zijn.