Uitwerking
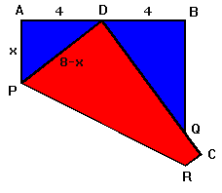In $\Delta$PDA geldt de stelling van Pythagoras:
$
\begin{array}{l}
x^2 + 4^2 = (8 - x)^2 \\
x^2 + 16 = 64 - 16x + x^2 \\
16x = 48 \\
x = 3 \\
\end{array}
$
Dat is al bijzonder. Het is een 3-4-5-driehoek.
Er geldt: $
\Delta PDA \sim \Delta DQB
$ Ga na!
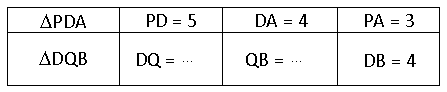
$\eqalign{DQ=\frac{20}{3}}$ en $\eqalign{QB=\frac{16}{3}}$
Er geldt: $
\Delta DQB \sim \Delta RQC
$
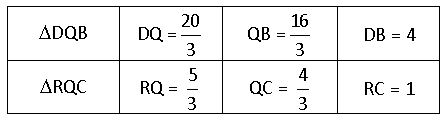
In driehoek PRZ geldt: DC = 8 en PZ = 4.
$
\begin{array}{l}
PR^2 = 4^2 + 8^2 = 16 + 64 = 80 \\
PR = \sqrt {80} = 4\sqrt 5 \\
\end{array}
$
Conclusie
$
PR = 4\sqrt 5
$