3. Haakjes
Hieronder zie je een rechthoek die zelf ook weer verdeeld is in rechthoeken. Je kunt de totale oppervlakte van die rechthoek op verschillende manieren berekenen.
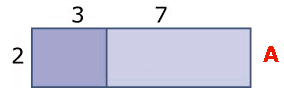
De oppervlakte van A bestaat uit een stuk van 6 en een stuk van 14, dat is samen 20. De oppervlakte is 20.
Je kunt ook eerst de lengte berekenen en dan de oppervlakte. De lengte is 3+7=10, dus de oppervlakte is 2×10=20.
Als je dat laatste in één keer wilt opschrijven dan moet je haakjes schrijven. Als je 2×3+7 zou schrijven, dan vergeet je waarschijnlijk dat die '7' ook keer '2' moet. Dus schrijven we beter 2×(3+7). Meestal laten we die '×' weg.
- De oppervlakte van figuur A is gelijk aan 2(3+7)=2·10=20
Nog meer haakjes
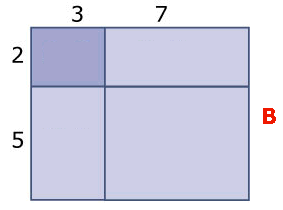
De oppervlakte van B bestaat zelfs uit 4 stukken: een stuk van 6, van 14, van 15 en een stuk van 35. Dat is samen gelijk aan 6+14+15+35=70.
Je kunt ook eerste de lengte en de breedte van de rechthoek berekenen en dan de oppervlakte. De lengte is 3+7=10 en de breedte is 2+5=7, dus de oppervlakte is 10·7=70.
Als je dat in één keer wilt opschrijven dan zou je 3+7 moeten vermenigvuldigen met 2+5. Je kunt dan niet schrijven 3+7·2+5 want dan gaat het vast niet goed. Je moet haakjes gebruiken.
- De oppervlakte van figuur B is gelijk aan (3+7)(2+5)=10·7=70
Variabelen
Wat je met getallen kunt, kan je ook met variabelen. Stel je voor dat je een rechthoek hebt van 2 bij x+7. De oppervlakte van de driehoek kan je dan schrijven als 2(x+7).
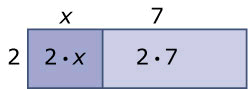
Als je naar de kleinere rechthoeken kijkt kan je ook zeggen dat de oppervlakte gelijk is aan 2x+14.
- 2(x+7)=2x+14
Dubbele haakjes
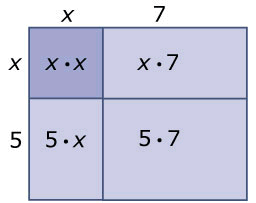
- (x+7)(x+5)=x2+7x+5x+35=x2+12x+35
Nog meer variabelen
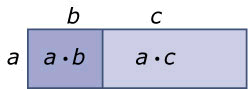
- a(b+c)=ab+ac
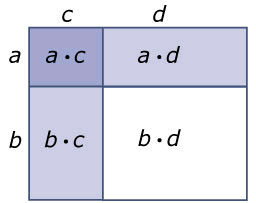
- (a+b)(c+d)=ac+ad+bc+bd
Theorie
In de wiskunde noemen we 'dingen' die je optelt termen. Het resultaat van een optelling noemen we som. Iets als 'p+1' noemen we een tweeterm omdat het uit twee termen bestaat.
'DIngen' die je vermenigvuldigt noemen we factoren. Een uitdrukking kan uit meerdere factoren bestaan. Zo bestaat p(p+2) uit de factoren 'p' en 'p+2'. De uitkomst van een vermenigvuldiging noemen het product.
De uitdrukking (p+1)(p+8) bestaat dus uit de factoren 'p+1' en 'p+8'. Die 'p+1' en 'p+8' zijn tweetermen. Dus je kunt zelfs zeggen dat (p+1)(p+8) het product is van twee tweetermen.
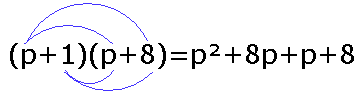
De som van termen en het product van factoren
In plaats van p2+8p+p+8 schrijf je p2+9p+8. Die '8p' en 'p' zijn gelijksoortigetermen. Dat betekent dat ze dezelfde variabelen hebben en gelijke exponenten. Het product van twee tweetermen kan een drieterm zijn.
Maar dat is niet altijd zo:
-
Het product van a+b en c+d is een vierterm.
(a + b)(c + d) = ac + ad + bc + bd -
Het product van (a-3)(a+3) is een tweeterm.
(a - 3)(a + 3) = a2 + 3a - 3a - 9 = a2 - 9 -
Het kwadraat van een tweeterm is een drieterm.
(x + 3)2 = (x + 3)(x + 3) = x2 + 6x + 9
Opdracht 3
Herleid onderstaande formules. Dat wil zeggen: schrijf de formules zonder haakjes en zo kort mogelijk.
$
\eqalign{
& a.\,\,\,8(h + 8) - 17 = \cr
& b.\,\,\, - \frac{1}
{4}\left( {12q + 28} \right) + 7 = \cr
& c.\,\,\,4k - 6\left( {\frac{1}
{2}k - 3} \right) = \cr
& d.\,\,\,6(a + 2b) + 2a = \cr
& e.\,\,\,a\left( {2a + c} \right) + a(3b - 2c) = \cr
& f.\,\,\, - (3p - 5q) + (p + q)^2 = \cr
& g.\,\,\,\left( {x - y} \right)^2 + 4xy = \cr
& h.\,\,\,(a - 3)(a + 5) - a^2 - 3 = \cr
& i.\,\,\,\left( {3x + y} \right)^2 + \left( {3x - y} \right)^2 = \cr}
$