Uitwerkingen
Van een rechthoekig terrein is de lengte 5 meter meer dan de breedte. De oppervlakte is 150 m2.
- Bereken de afmetingen van het terrein.
Oplossing
Als je de breedte x noemt dan is de lengte x+5.
Er geldt: x(x+5)=150.
Deze vergelijking kan je dan oplossen.
Opgave 2
Van een rechthoekig terrein is de omtrek gelijk aan 120 m. De lengte is twee keer zo groot als de breedte.
- Bereken de afmetingen van het terrein.
Oplossing
Noem de breedte x, dan is de lengte gelijk aan 2x. De omtrek is dan 6x. Met 6x=120 vind je dan x=20.
De breedte is 20 m en de lengte is 40 m.
Opgave 3
Neem 's aan dat je 200 m prikkeldraad hebt.
- Wat is de oppervlakte van het grootst mogelijke terrein dat je daarmee kan afzetten!?
Oplossing
Strikvraag!:-)
Opgave 4
Hieronder zie je het trapezium ABCD met twee rechte hoeken.
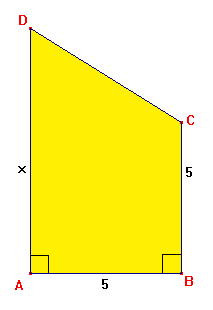
- Geef een formule voor de oppervlakte van ABCD.
- Wat is x als de oppervlakte gelijk is aan 30.
Oplossing
Teken eerst een hulplijn.
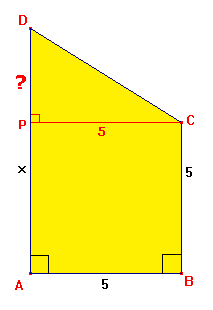
De lengte van het stuk met het vraagteken is gelijk aan x-5. De oppervlakte wordt:
$
Opp = 25 + \frac{1}
{2} \cdot 5 \cdot \left( {x - 5} \right) = 2\frac{1}
{2}x + 12\frac{1}
{2}
$
Als de oppervlakte 30 is dan geldt:
$
\eqalign{
& 2\frac{1}
{2}x + 12\frac{1}
{2} = 30 \cr
& 5x + 25 = 60 \cr
& 5x = 35 \cr
& x = 7 \cr}
$
Opgave 5
Hieronder zie je het trapezium ABCD nog een keer.

- Geef een formule voor de omtrek van ABCD.
- Wat is x als de omtrek gelijk is aan 20?
Oplossing
Voor de omtrek zou je schuine zijde van driehoek PCD moeten uitdrukken in x.
$
CD = \sqrt {5^2 + \left( {x - 5} \right)^2 } = \sqrt {x^2 - 10x + 50}
$
De omtrek is dan gelijk aan:
$
Omtrek = x + 10 + \sqrt {x^2 - 10x + 50}
$
Als de omtrek 20 is dan is x=5.
Een vergelijking oplossen was niet nodig, maar 't kan wel:
$
\eqalign{
& x + 10 + \sqrt {x^2 - 10x + 50} = 20 \cr
& x + \sqrt {x^2 - 10x + 50} = 10 \cr
& \sqrt {x^2 - 10x + 50} = 10 - x \cr
& x^2 - 10x + 50 = (10 - x)^2 \cr
& x^2 - 10x + 50 = 100 - 20x + x^2 \cr
& - 10x + 50 = 100 - 20x \cr
& 10x = 50 \cr
& x = 5 \cr}
$
Opgave 6
Drie zijden van een gelijkbenig trapezium zijn 10 cm lang.
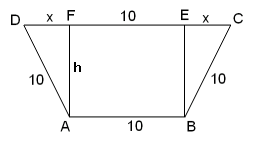
- Geef een formule voor de oppervlakte van het trapezium, uitgedruk in x.
Oplossing
De oppervlakte van het trapezium is gelijk aan:
$
\eqalign{
& Opp. = \frac{{z_1 + z_2 }}
{2} \cdot h \cr
& z_1 = 10 \cr
& z_2 = 10 + 2x \cr
& h = \sqrt {10^2 - x^2 } \cr
& Opp. = \frac{{10 + 10 + 2x}}
{2} \cdot \sqrt {10^2 - x^2 } \cr
& Opp. = \left( {10 + x} \right) \cdot \sqrt {10^2 - x^2 } \cr}
$
Opgave 7
In een balk ABCD.EFGH is de lengte twee keer zo groot als de breedte. De hoogte is drie keer zo groot als de breedte.
- Noem de breedte 'x' en druk de lengte van de lichaamsdiagonaal AG uit in x.
-
Neem aan dat AG=$
\sqrt {42}
$
Bereken de afmetingen van de balk.
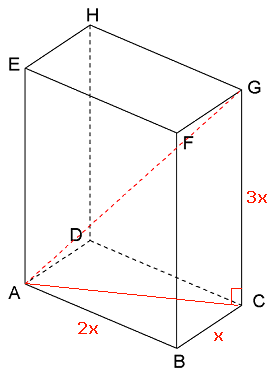
Oplossing
Bereken eerst AC:
$
AC = \sqrt {x^2 + \left( {2x} \right)^2 }
$
$
AC= \sqrt {x^2 + 4x^2 }
$
$
AC = \sqrt {5x^2 }
$
Bereken AG:
$
AG = \sqrt {\left( {\sqrt {5x^2 } } \right)^2 + \left( {3x} \right)^2 }
$
$
AG = \sqrt {5x^2 + 9x^2 }
$
$
AG = \sqrt {14x^2 }
$
$
\eqalign{
& \sqrt {14x^2 } = \sqrt {42} \cr
& 14x^2 = 42 \cr
& x^2 = 3 \cr
& x = \sqrt 3 \,\,\left( {of\,\,x = - \sqrt 3 \,\,v.n.} \right) \cr}
$