
Symmetrie bij functies
Lijnsymmetrie
De grafiek van f heeft de lijn x=a als symmetrie-as als voor elke waarde van p geldt:
Met a+p en a-p beide behorend bij het domein van f
|
Voorbeeld
$
\eqalign{
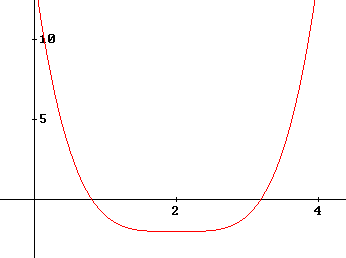
& f(x) = (x - 2)^4 - 2 \cr
& Heeft\,\,als\,\,symmetrie - as:x = 2 \cr
& Er\,\,geldt:f(2 + p) = f(2 - p)\,\,voor\,\,p \in R \cr
& f(2 + p) = f(2 - p) \cr
& (2 + p - 2)^4 - 2 = (2 - p - 2)^4 - 2 \cr
& p^4 - 2 = \left( { - p} \right)^4 - 2 \cr
& Klopt! \cr}
$ |
 |
Puntsymmetrie
De grafiek van f is puntsymmetrisch in het punt (a,b) als het gemiddelde van f(a+p) en f(a-p) gelijk is aan b voor elke waarde van p.
Met a+p en a-p behorend tot het domein van f.
|
Voorbeeld
$
\eqalign{
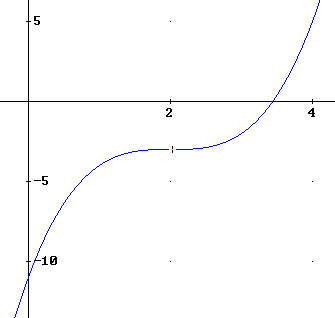
& f(x) = \left( {x - 2} \right)^3 - 3 \cr
& Is\,\,puntsymmetrisch\,\,in\,\,(2, - 3): \cr
& Er\,\,geldt:\frac{{f(2 + p) + f(2 - p)}}
{2} = - 3 \cr
& \frac{{\left( {2 + p - 2} \right)^3 - 3 + \left( {2 - p - 2} \right)^3 - 3}}
{2} = \cr
& \frac{{\left( p \right)^3 - 3 + \left( { - p} \right)^3 - 3}}
{2} = \cr
& \frac{{p^3 - 3 - p^3 - 3}}
{2} = \cr
& \frac{{ - 6}}
{2} = - 3 \cr
& Klopt! \cr}
$ |
 |
|
|
