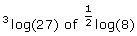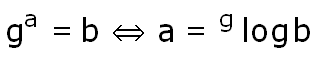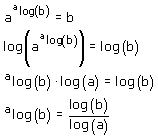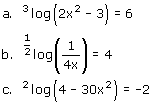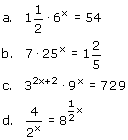1. LogaritmenWe zagen al eerder dat je bij het vermenigvuldigen van machten met gelijk grondtal de exponenten op kan tellen. Dat is bijzonder, want als je bij een willekeurige vermenigvuldiging de getallen zou kunnen schrijven als machten van bijvoorbeeld 2 dan zou je de exponenten kunnen optellen... en dus kunnen 'vermenigvuldigen zonder te vermenigvuldigen'.
Bereken op dezelfde manier:
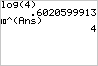
Logaritmen Dat lijkt handig maar de praktische toepasbaarheid valt nogal tegen, want niet alle getallen zijn op een eenvoudige manier te schrijven als machten van 2. Je zou dan voor 'alle getallen' lijsten moeten gaan maken... Dat lijkt niet zo zinvol, maar in de praktijk (voor de uitvinding van de rekenmachine) bestonden die lijsten wel degelijk! In tabellenboekjes kan je dit soort lijsten vinden, maar dan wel met grondtal 10. Deze getallen heten logaritmen en geloof het of niet die logaritmen zijn nog steeds hele nuttige 'dingen'. Ze worden nog steeds veel gebruikt... De uitdrukking log(4) geeft de exponent als je 4 als macht van 10 zou schrijven, dus: 10...=4. Met je GR kan je makkelijk een benadering vinden voor dit getal.
Op je GR zit het knopje [LOG] waarmee je dus de logaritmen met grondtal 10 kan benaderen. Anders gezegd als je praat over LOG dan praat je over logaritmen met het grondtal 10. Maar je kunt voor elk willekeurig grondtal met logaritmen rekenen (g>0 en g¹1), dus ook met grondtal 3 of 1/2. Je schrijft dan het grondtal bij de logaritme:
Maar voor alle logaritme geldt in ieder geval de hoofdregel:
(met g>0 en g¹1 en b>0) Veel rekenregels voor de logaritmen kan je hier uit af leiden. Probleem Nu is echter het probleem dat je GR geen functie heeft voor logaritmen met een ander grondtal dan 10 of e. Dus als je uit zou willen rekenen wat 2log(8) of 3log(81) is dan gaat dat niet 'zomaar'. Daar moet je eerst iets voor doen. Er geldt:
Het 'bewijs':
Voorbeelden
Bereken op 3 decimalen nauwkeurig:
Bereken exact:
Los op:
Los op:
|
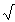 256=
256=