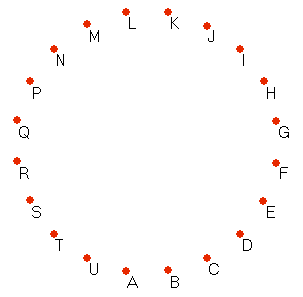
Stel je voor dat er 20 mensen in een ruimte zijn en dat iedereen elkaar de hand schud. Hoeveel keer moeten er dan handen worden geschud? Grafen Je kunt dit probleem oplossen met grafen. Teken 20 punten en zet lijnen voor elke ‘handschud’:
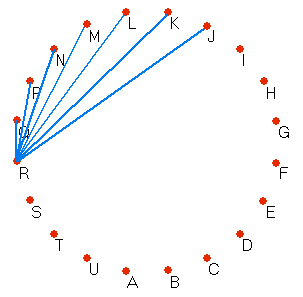
Als je nu lijntjes tekent vanuit Q heb je nog 18 mogelijkheden over, want het lijntje naar R heb je al.
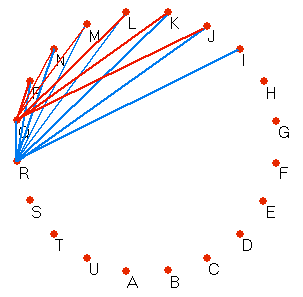
Als je zo door gaat dan moet je uiteindelijk Hoeveel lijntjes zijn dat in totaal? Vierkanten
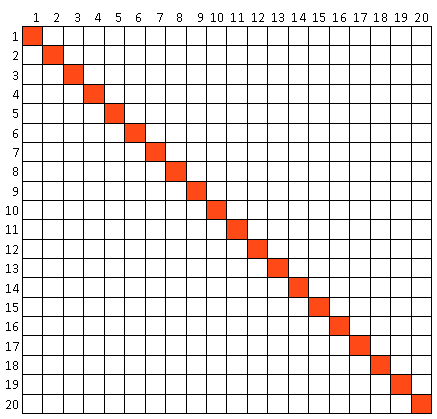
Je kunt het probleem ook oplossen met een vierkant. Zet de getallen 1 t/m 20 horizontaal en verticaal in een tabel.
Dat zouden dan 400 ‘handschudden’ zijn, maar dat klopt natuurlijk niet, want je kunt je zelf wel een hand geven maar dat telt niet.
De vakjes op de diagonaal vallen af. Maar nu tellen we alles dubbel. We gebruiken alleen de vakjes onder de diagonaal. Hoeveel witte vakjes zitten er onder de diagonaal?
Formule maken
Nu je gezien hebt hoe je dat met een tabel doet zou je dan niet een formule kunnen bedenken? Bij 20 mensen moet je 202 hokjes tekenen. Daar trek je dan 20 van af. Je deelt door 2 en je krijgt dan 190 hokjes. Bij n mensen moet je n2 hokjes tekenen. Daar trek je dan n hokjes van af. Je deelt door 2 en je krijgt $\eqalign{\frac{n^2-n}{2}}$ hokjes. Berekenen met de formule hoeveel handen er geschud worden bij 30 mensen.
Een andere manier om een formule te vinden
Je kan de formule ook op een andere manier vinden. Als er 20 mensen in een ruimte zijn dan moet iedereen 19 andere mensen een hand geven. Dat is in totaal 20·19=380 keer. Maar dan tel je alle handenschudden dubbel. Ga dat na! Je moet dus nog delen door 2. Dat geeft 190 keer handenschudden.
Vind op dezelfde manier een formule voor n mensen.
Toepassing
We hadden al gezien dat die 190 hetzelfde is als 19+18+17+…+2+1. We hebben nu (ook) een formule om de som van zo’n rijtje getallen op te tellen. Stel je voor dat je de getallen 1 t/m 999 zou willen optellen. Ga na dat dit de ‘som’ is die hoort bij het handenschudprobleem met 1000 mensen. Volgens de formule is de oplossing gelijk aan:
$
\eqalign{\frac{{1000^2 - 1000}}{2}}$ = ${\rm{499}}{\rm{.500}} Bereken de som van de getallen 1 t/m 9.999
|