logaritmische schalen

Logaritmische schaalverdeling Van een gewone schaalverdeling maar je logaritmische schaalverdeling door elk getal $n$ te vervangen door $10^n$: Het voordeel van een logaritmische schaalverdeling is dat je waarnemingen kunt uitzetten die sterk in grootte verschillen.
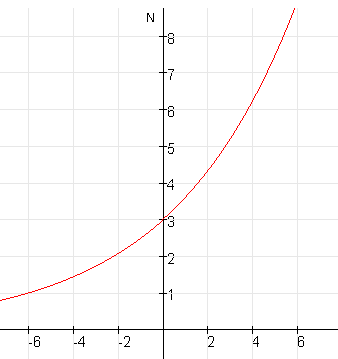
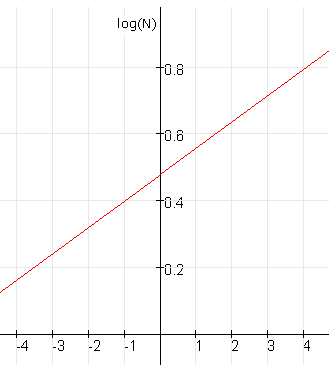
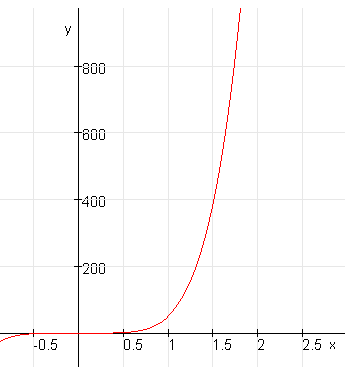
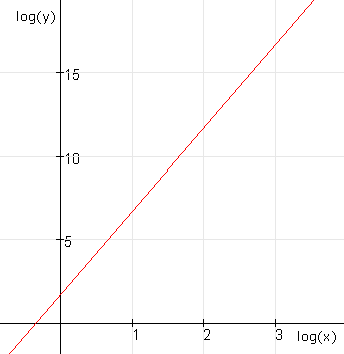
Logaritmisch papier Je ziet hieronder de grafiek van: $ N = 3 \cdot 1,2^t $: Als je voor de verticale as niet $N$ zet maar $log(N)$ krijg je deze grafiek: De grafiek is dan een rechte lijn.	Dubbellogaritmisch papier Je ziet hieronder de grafiek van: $ y = 50 \cdot x^5 $ Als je op de verticale as niet $N$ zet maar $log(N)$ en op horizontale as niet $x$ maar $log(x)$ krijg je deze grafiek: De grafiek is dan een rechte lijn.
Exponentiële formules omwerken Je kunt: $ N = b \cdot g^t $ schrijven als: $ \log (N) = pt + q $ Voorbeeld $ \begin{array}{l} N = 3 \cdot 1,2^t \\ \log (N) = \log (3 \cdot 1,2^t ) \\ \log (N) = \log (3) + \log (1,2^t ) \\ \log (N) = \log (3) + t \cdot \log (1,2) \\ \log (N) = \log (1,2) \cdot t + \log (3) \\ benaderd: \\ \log (N) = {\rm{0}}{\rm{,079\cdot t + 0}}{\rm{,477}} \\ \end{array} $	Machtsformules omwerken Je kunt: $ y = ax^n $ schrijven als: $ \log (y) = p + q \cdot \log (x) $ Voorbeeld $ \begin{array}{l} {\rm{y = 50}} \cdot {\rm{x}}^{\rm{5}} \\ \log (y) = \log (50 \cdot {\rm{x}}^{\rm{5}} ) \\ \log (y) = \log (50) + \log ({\rm{x}}^{\rm{5}} ) \\ \log (y) = \log (50) + 5 \cdot \log (x) \\ benaderd: \\ \log (y) = {\rm{1}}{\rm{,699}} + 5 \cdot \log (x) \\ \end{array} $
Formule met logaritmen omwerken (1) Je kunt bovenstaande omzetting ook in omgekeerde volgorde doen: $ \begin{array}{l} \log (N) = 0,2t + 3,1 \\ N = 10^{0,2t + 3,1} \\ N = 10^{0,2t} \cdot 10^{3,1} \\ N = 10^{3,1} \cdot \left( {10^{0,2} } \right)^t \\ benaderd: \\ N = {\rm{1259}} \cdot {\rm{1}}{\rm{,585}}^{\rm{t}} \\ \end{array} $	Formule met logaritmen omwerken (2) Je kunt bovenstaan omzetting ook in omgekeerde volgorde doen: $ \begin{array}{l} \log (K) = 2,8 + 4,9 \cdot \log (L) \\ \log (K) = \log (10^{2,8} ) + \log (L^{4,9} ) \\ \log (K) = \log (10^{2,8} \cdot L^{4,9} ) \\ K = 10^{2,8} \cdot L^{4,9} \\ benaderd: \\ K = {\rm{631}} \cdot L^{4,9} \\ \end{array} $
Logaritmisch papier - exponentieel verband De grafiek van een exponentieel verband wordt op enkellogaritmisch papier weergegeven als een rechte lijn. Je kunt vanuit een rechte lijn op enkellogaritmisch papier de formule afleiden Je kunt een functie tekenen op enkellogaritmisch papier.	Logaritmisch papier - machtsverband De grafiek van een machtsverband wordt op dubbellogaritmisch papier weergegeven als een rechte lijn. Je kunt vanuit een rechte lijn op dubbellogaritmisch papier de formule afleiden Je kunt een functie tekenen op dubbellogaritmisch papier.