





Oplossing week 2
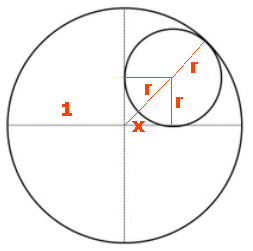
$\begin{array}{l}\left\{ \begin{array}{l}2r^2 = (x + r)^2 \\ x + 2r = 1 \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2r^2 = (x + r)^2 \\ x = 1 - 2r \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2r^2 = (1 - 2r + r)^2 \\ x = 1 - 2r \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2r^2 = (1 - r)^2 \\ x = 1 - 2r \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2r^2 = 1 - 2r + r^2 \\ x = 1 - 2r \\ \end{array} \right. \\ \left\{ \begin{array}{l} r^2 + 2r - 1 = 0 \\ x = 1 - 2r \\ \end{array} \right. \\ \left\{ \begin{array}{l} r = - 1 + \sqrt 2 \\ x = 3 - 2\sqrt 2 \\ \end{array} \right. \vee \left\{ \begin{array}{l} r = - 1 - \sqrt 2 \\ x = 3 + 2\sqrt 2 \\ \end{array} \right.(v.n.) \\ \end{array}$
De straal van de kleine cirkel is gelijk aan $
- 1 + \sqrt 2
$
©2004-2025 W.v.Ravenstein