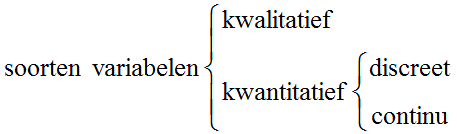|
Soorten variabelen
Bij kwantitatieve gegevens gaat het om meetbare gegeven, zoals temperatuur, snelheid of gewicht.
Een kwantitatieve variabele wordt uitgedrukt in een getal. Het verschil tussen twee van deze opeenvolgende getallen heeft een eenduidige betekenis.
|
Discreet of continu
Bij een discrete variabele worden alleen maar 'losse' waarden aangenomen. Tussenwaarden hebben geen betekenis.
Bij continue variabelen kunnen alle waarden op een interval worden aangenomen.
|
|
Nominaal, ordinaal, interval en rationiveau
Bij de statistiek kom je vaak de volgende indeling tegen:
-
Nominaal
Hier heeft de waarde die een variabele kan aannemen alleen de betekenis van een naam. Er is geen sprake van een volgorde. Denk bijvoorbeeld aan rugnummers van een voetbal elftal. Je kunt niet zeggen dat de speler met rugnummer 14 beter is dan de speler met rugnummer 7.
-
Ordinaal
Een waarde op ordinaal niveau geeft alleen een volgorde aan. Denk bijvoorbeeld aan opleiding. Voorbeeld
-
=MBO
-
=HBO
-
=UNIVERSITEIT
Er is wel sprake van volgorde, een hoger nummer duidt op een hogere opleiding, maar het verschil tussen bijvoorbeeld 1 en 2 is niet hetzelfde als het verschil tussen 2 en 3.
-
Interval
Bij variabelen op intervalniveau hebben verschillen wel een betekenis. Neem bijvoorbeeld temperatuur. Het verschil tussen 30° en 40° is hetzelfde als het verschil tussen 70° en 80°. Je kunt echter niet zeggen dat 80° twee keer zo warm is als 40°.
-
Ratio
Bij variabelen op rationiveau heb je altijd een nulpunt. Denk aan gewicht, lengte of het aantal verkochte exemplaren van een product. Je kunt uitspraken doen 'A scoort twee keer zo hoog als B'.
|
Nominaal, ordinaal, interval en rationiveau
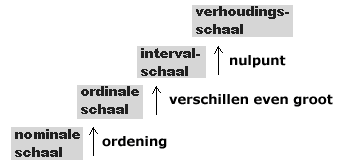
Zoals je ziet, komt er bij elk niveau hoger een eigenschap bij
Opmerking uit het boek
"Men maakt bij kwantitatieve variabelen onderscheid tussen variabelen op intervalniveau en op rationiveau, maar deze begrippen hoef je niet te kennen op het centraal examen."
getal & ruimte - havo wiskunde A deel 3 - pagina 54
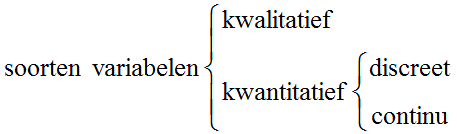

|
|
De normale verdeling
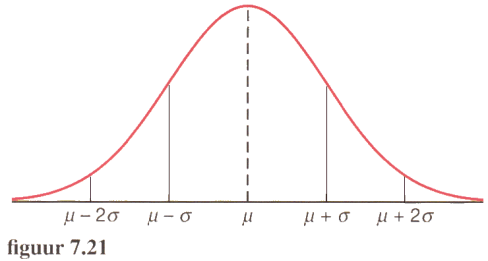
Een paar eigenschappen van een normale verdeling:
-
klokvormig
-
symmetrisch t.o.v. het gemiddelde.
-
gemiddelde, mediaan en modus vallen samen
-
de verdeling wordt bepaald door de verwachtingswaarde en de standaarddeviatie
Vuistregels bij de normale verdeling
-
68% van de gegevens wijkt op z'n hoogst één keer de standaarddeviatie af van de verwachtingswaarde
-
95% van wijkt op z'n hoogst twee keer de standaarddeviatie af van de verwachtingswaarde
|
Voorbeeld

Het gewicht van de mandarijnen uit een grote partij is normaal verdeeld met een gemiddelde van 80 gram. Verder is bekend dat 16% van de mandarijnen minder dan 76 gram weegt.
-
Bereken de standaardafwijking
Uitwerking
16% weegt minder dan 76 gram, dus 76 ligt één standaardafwijking van het gemiddelde af. De standaardafwijking is 80-76=4 gram.
|