The President`s Proof

There are many proofs to the Pythagorean theorem. President James Garfield developed his own proof in The Journal of Education (Volume 3 issue161) in 1876. President Garfield studied math at Williams College (in Williamstown, MA) and taught in the public school in Pownal, Vermont, for a year or two after graduating. President Garfield may have been joking when he stated about his proof that, "we think it something on which the members of both houses can unite without distinction of the party." A nice feature of mathematical proofs is that they are not subject to political opinion.

Prove the Pythagorean theorem using the method developed by President James Garfield.

See Figure 3. Starting with the right triangle ABC, construct a line perpendicular to BC and through the point C. Extend AC from the point C.

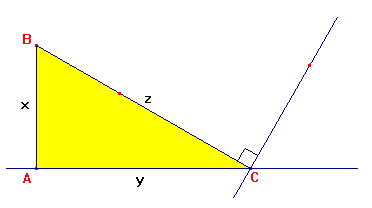
Figure 3. Diagram of triangle ABC for use in the president`s proof.

Now look at Figure 4. Draw a circle with center C and radius equal to the length of BC. Label the point E as the point where the circle and the perpendicular line intersect. Draw a line through E and perpendicular to AC and label the intersection point D. Lastly, draw the segment BE.

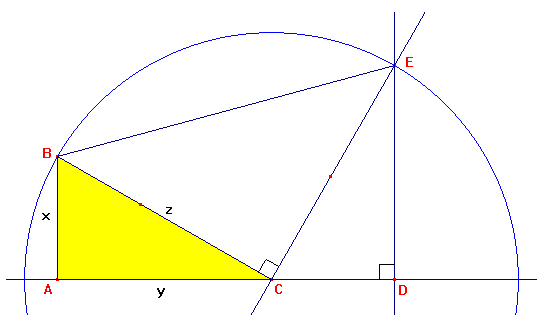
Figure 4. Diagram for use with the president`s proof.

---

Questions

---

1. What can you say about triangles ABC and CDE?
2. What is the area of triangle ABC? Triangle BCE? Triangle CDE?
3. What type of quadrilateral is ABED?
4. What is the area of ABED?
5. What can be said about the sum of the area of triangles ABC, BCE, and CDE and the area of ABED?
6. Using only x`s, y`s and z`s, write an equation for the sum of the area of triangles ABC, BCE, and CDE and for the area of ABED.
7. Solve the equation you found in problem 6.
8. What have you proven?

®bron