|
Vergelijkingen en bijzondere rechthoekige driehoeken
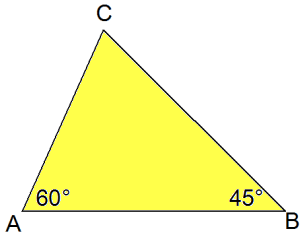
De omtrek van driehoek ABC in 12.
-
Bereken AB in drie decimalen nauwkeurig
|
Vergelijkingen en de stelling van Pythagoras
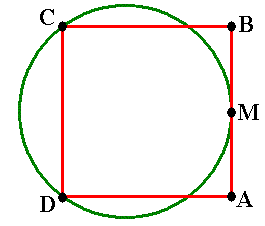
Het rode vierkant heeft een zijde van 8. Het punt M is het midden van AB en de groene cirkel gaat door de punten C, D en M.
-
Bereken exact de straal van deze cirkel
|
|
Uitwerking
Teken de hoogtelijn CD. Je krijgt dan twee bijzondere rechthoekige driehoeken (de tekendriehoeken!).
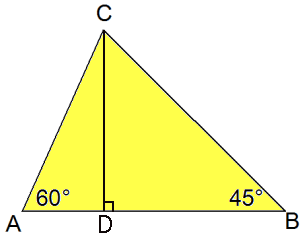
Neem $AD=x$. Dan is $AC=2x$ en $CD=x\sqrt{3}$, maar dan is $DB=x\sqrt{3}$ en kan je berekenen dat $BC=x\sqrt{6}$.
De omtrek is 12, er geldt:
$\eqalign{
& x + 2x + x\sqrt 6 + x\sqrt 3 = 12 \cr
& 3x + x\sqrt 6 + x\sqrt 3 = 12 \cr
& x\left( {3 + \sqrt 6 + \sqrt 3 } \right) = 12 \cr
& x = \frac{{12}}{{3 + \sqrt 6 + \sqrt 3 }} \cr
& x \approx {\text{1}}{\text{,6710}} \cr
& AD = {\text{1}}{\text{,6710}} + {\text{1}}{\text{,6710}} \cdot \sqrt 3 \cr
& AD \approx 4,565 \cr} $
|
Uitwerking
Het is hier handig om het middelpunt van de cirkel te tekenen en aan te geven welke lijnstukken je nodig hebt. Gebruik waar mogelijk de straal van de cirkel. Je krijgt:
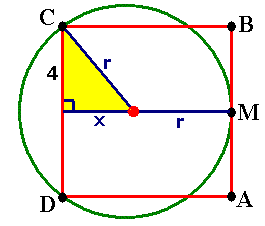
Er geldt:
$x+r=8$
$r^2=x^2+16$
Oplossen geeft:
$r^2=(r-8)^2+16$
$r^2=r^2-16r+64+16$
$16r=80$
$r=5$
|