|
Optimaliseren met behulp van de afgeleide
In de praktijk gaat het bij problemen vaak om het vinden van een maximum of een minimum. Voorbeelden van zulk optimaliseringsproblemen zijn:
-
Bij welke afmetingen is de oppervlakte bij een gegeven omtrek het grootst?
-
Wat zijn de afmetingen van de doos met de grootste inhoud dit je uit een rechthoekig stuk karton kan maken?
-
Bij welk route horen de laagste kosten?
Het gebruik van de afgeleide ligt dan voor de hand. Let op of je mag benaderen (met je GR) of dat er een exact antwoord wordt gevraagd.
Notaties voor de afgeleide van $y=f(x)$


|
Optimaliseren van oppervlakten bij grafieken
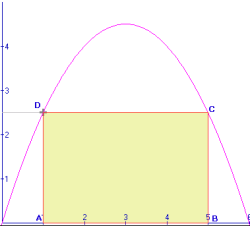
Gegeven is de functie $f(x)=-0,5x^2+3x$.
Van een rechthoek $ABCD$ liggen de punten $A$ en $B$ op de x-as en de punten $C$ en $D$ op de grafiek van $f$.
Als je $p=x_A$ neemt dan kan je de omtrek en de oppervlakte van $ABCD$ uitdrukken in $p$.
Met de afgeleide zou je dan de maximale omtrek of de maximale oppervlakte kunnen berekenen.
|
|
Voorbeeld 1
Je hebt een rechthoekig stuk karton met afmetingen 80 cm bij 50 cm. Daaruit moet je een doos vouwen (zonder deksel!) met een zo groot mogelijke inhoud.
Je moet uit de vier hoeken van de rechthoek een stukje knippen om de doos te vormen.
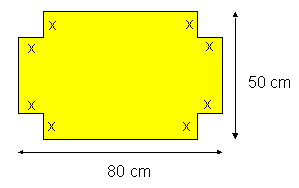
-
Bereken met de afgeleide hoe groot dat stukje moet zijn zodat de doos een maximale inhoud heeft.
|
Voorbeeld 2
Gegeven is de functie $f(x)=(x-4)^2$. Onder de grafiek tekenen we een rechthoek $OABC$ met $O(0,0)$ en $A(p,0)$ met 0$\le$p$\le$4. $B$ ligt op de grafiek van $f$ en $C$ ligt op de $y$-as.
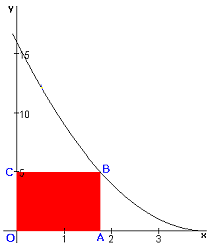
-
Druk de oppervlakte van $OABC$ uit in $p$.
-
Bereken m.b.v. differentiëren de maximale oppervlakte van $OABC$.
|