|
De boxplot
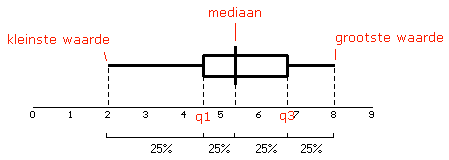
Een boxplot is een grafische voorstelling waarmee je snel een overzicht van de verdeling van een verzameling gegevens kunt krijgen. Met boxplots kun je makkelijk verschillende verdelingen vergelijken.
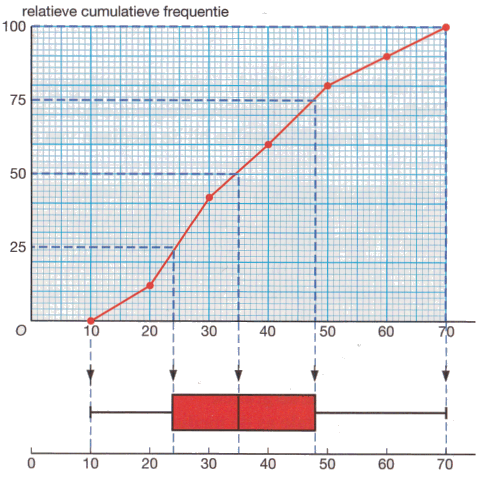
Hieronder staat een voorbeeld.
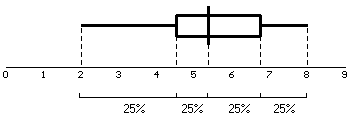
In een boxplot kan je de kwartielen, de mediaan en de grootste en de kleinste waarde aflezen.
|
De boxplot en de GR
Je kunt met de GR allerlei kengetallen van een rijtje getallen of een klassenverdeling berekenen.
Je moet bij proeven, SO's en examens wel uitleggen wat je hebt ingevoerd en hoe je 'dingen' berekend hebt.
Hieronder je uitleg vinden over berekeningen met de CASIO. Er zijn twee verschillende soorten berekeningen die je nodig hebt.
Een rijtje getallen
Als je van een rijtje getallen centrum- en/of spreidingsmaten wilt berekenen dan gebruikt je één lijstje van je GR:
Een frequentieverdeling
Als je van een frequentieverdeling de centrum- en/of spreidingsmaten wilt berekenen dan gebruik je twee lijstjes. Een lijstje met de waarnemingsgetallen en een lijstje met de frequenties.
|
|
Spreidingsbreedte en kwartielafstand
Om een goede indruk te krijgen van een serie waarnemingsgetallen moet je behalve het gemiddelde of de mediaan ook nog een maat hebben dat informatie geeft over de spreiding van de getallen. Zo'n getal heet een spreidingsmaat.
-
De spreidingbreedte is het verschil tussen het grootste en het kleinste waarnemingsgetal.
-
De interkwartielafstand, kortweg kwartielafstand, is het verschil tussen het derde en eerste kwartiel.

Het verschil tussen de grootste en de kleinste waarde is de spreidingsbreedte. Het verschil tussen q3 en q1 is de kwartielafstand. |
De standaardafwijking
De spreidingsmaat die het meest gebruikt wordt is de standaarddeviatie of in goed Nederlands standaardafwijking.
Om de standaarddeviatie (van een populatie) te berekenen neem je de volgende stappen:
-
Bereken het gemiddelde.
-
Neem van elk getal de afstand tot het gemiddelde
-
Neem het kwadraat van die afstanden.
-
Bereken het gemiddelde van die kwadraten.
-
Neem de wortel van de uitkomst
Hoe groter de standaarddeviatie hoe groter de verschillen tussen de verschillende waarnemingen.
Met de GR kan je handig $\overline x$, $n$ en $\sigma$ berekenen. Kijk in 't lijstje getallen van je GR naar $\sigma_x$.
|